
公安部最新修订的《机动车驾驶证申领和使用的规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二),只有三个科目都过关后才能拿到驾驶证,某驾校现有100名新学员,第一批参加的20人各科目通过的人数情况如下表:
| 参考人数 | 通过科目一人数 | 通过科目二人数 | 通过科目三人数 |
| 20 | 12 | 4 | 2 |
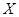 为学校因为该学员而奖励教官的金额数,求
为学校因为该学员而奖励教官的金额数,求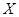 的数学期望。
的数学期望。 科目:高中数学 来源: 题型:解答题
了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成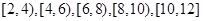 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(Ⅰ)求实数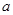 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
(Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀
的概率;
(Ⅲ)若从此次测试成绩最好和最差的两组男生中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(注:方差s2=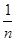 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2]),其中
)2]),其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
给出施化肥量(kg)对水稻产量(kg)影响的试验数据:
| 施化肥量x | 15 | 20 | 25 | 30 |
| 水稻产量y | 330 | 345 | 365 | 405 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的
频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,
1 500)).
(1)求居民收入在[3 000,3 500)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中按分层抽样方法抽出100人作进一步分析,则月收入在[2 500,3 000)的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年元旦、春节前夕,各个物流公司都出现了爆仓现象,直接原因就是网上疯狂的购物.某商家针对人们在网上购物的态度在某城市进行了一次调查,共调查了124人,其中女性70人,男性54人.女性中有43人对网上购物持赞成态度,另外27人持反对态度;男性中有21人赞成网上购物,另外33人持反对态度.
(Ⅰ) 估计该地区对网上购物持赞成态度的比例;
(Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关;
附:表1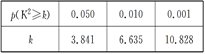
K2=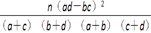
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行运动会,组委会招墓了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下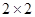 列联表:
列联表: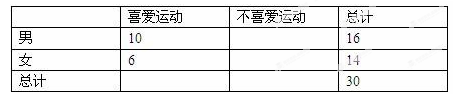
(2)根据列联表的独立性检验,有多大的把握认为性别与喜爱运动有关?
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率。
参考公式: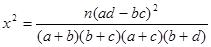 (其中
(其中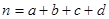 )
)
| | 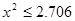 |  |  | 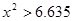 |
| 是否有关联 | 没有关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
(2)若从所有“运动健将”中选3名代表,求所选代表中女“运动健将”恰有2人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com