
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:
①![]() ; ②
; ② ![]() ;
;
③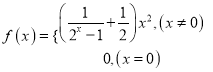 ; ④
; ④![]() .
.
则其中是“偏对称函数”的函数为__________.
【答案】②④
【解析】由当![]() ,且
,且![]() 时,都有
时,都有![]() 可得
可得![]() 或
或![]() ,即条件②等价于函数
,即条件②等价于函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
对于![]() ,显然满足①,且易证
,显然满足①,且易证![]() 是偶函数,当
是偶函数,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,因为
上单调递增,因为![]() 是偶函数,所以
是偶函数,所以![]() 在
在![]() 上单调递减,满足条件②,由
上单调递减,满足条件②,由![]() 是偶函数可得当
是偶函数可得当![]() ,且
,且![]() 时,
时, ![]() ,故不满足条件③;
,故不满足条件③;
对于![]() ,显然满足条件①,当
,显然满足条件①,当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时, ![]() ,由复合函数单调性法则可知
,由复合函数单调性法则可知![]() 在
在![]() 上单调递减,故满足条件②,由函数的单调性可知,当
上单调递减,故满足条件②,由函数的单调性可知,当![]() 时,且
时,且![]() 时,
时, ![]() ,不妨设
,不妨设![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
, ![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() 满足条件③;
满足条件③;
对于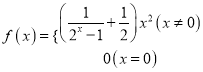 ,易证
,易证![]() 是奇函数,由奇函数的性质可得,
是奇函数,由奇函数的性质可得, ![]() 在
在![]() 和
和![]() 上的单调性相同,故不满足②;
上的单调性相同,故不满足②;
对于![]() ,显然满足条件①,
,显然满足条件①, ![]() ,则
,则![]() ,满足条件②,由
,满足条件②,由![]() 的单调性知当
的单调性知当![]() 时,且
时,且![]() 时,
时, ![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
, ![]() ,
, ![]()
令![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,取等号,所以
时,取等号,所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,满足条件③;
,满足条件③;
故答案为②④


科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
科目:高中数学 来源: 题型:
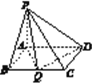
【题目】在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=![]() BC(a>0).
BC(a>0).
(1)当a=1时,求证:BD⊥PC;
(2)若BC边上有且只有一个点Q,使得PQ⊥QD,求此时二面角A-PD-Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)=-f(x)且f(x)在[-1,0]上是增函数,给出下列四个命题:
①f(x)是周期函数;②f(x)的图象关于x=1对称;③f(x)在[1,2]上是减函数;④f(2)=f(0).
其中正确命题的序号是____________.(请把正确命题的序号全部写出来)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图与侧视图是腰长为6的等腰直角三角形,俯视图是正方形.
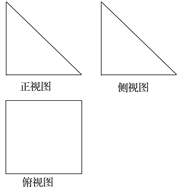
(1)请画出该几何体的直观图,并求出它的体积;
(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1?如何组拼?试证明你的结论;
(3)在(2)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com