
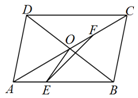
 已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.
已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.分析 (I)$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AE},\overrightarrow{BD}$,代入平面向量的数量积公式运算即可;
(II)利用余弦定理求出cos∠BAD,根据(I)得出$\overrightarrow{AE}=\frac{1}{3}\overrightarrow{AB}$,设$\overrightarrow{AF}=y\overrightarrow{AC}$,得出$\overrightarrow{AF}•\overrightarrow{EF}$关于y的二次函数,从而得出最小值.
解答 解:(Ⅰ)由平行四边形ABCD知OA=OC,OB=OD,
∴$\overrightarrow{AO}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$,
∵$\overrightarrow{AE}=\overrightarrow{AO}+\overrightarrow{OE}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}+\overrightarrow{OE}$,
∴$\overrightarrow{AE}•\overrightarrow{BD}=(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}+\overrightarrow{OE})•\overrightarrow{BD}=(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD})•(\overrightarrow{AD}-\overrightarrow{AB})+\overrightarrow{OE}•\overrightarrow{BD}$,
而$\overrightarrow{OE}•\overrightarrow{BD}=0$,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,
∴$\overrightarrow{AE}•\overrightarrow{BD}=\frac{1}{2}{\overrightarrow{AD}^2}-\frac{1}{2}{\overrightarrow{AB}^2}=-\frac{5}{2}$.
(Ⅱ)∵$|\overrightarrow{BD}|=\sqrt{10}$,
∴${\overrightarrow{BD}^2}={(\overrightarrow{AD}-\overrightarrow{AB})^2}=4+9-2×2×3cos∠BAD=10$,
∴$cos∠BAD=\frac{1}{4}$,
∴${\overrightarrow{AC}^2}={(\overrightarrow{AB}+\overrightarrow{AD})^2}=4+9+2×2×3cos∠BAD=16$,$\overrightarrow{AB}•\overrightarrow{AD}=\frac{3}{2}$,
设$\overrightarrow{AE}=x\overrightarrow{AB}$,由(Ⅰ)$\overrightarrow{AE}•\overrightarrow{BD}=-\frac{5}{2}=x\overrightarrow{AB}•(\overrightarrow{AD}-\overrightarrow{AB})=x\overrightarrow{AB}•\overrightarrow{AD}-x{\overrightarrow{AB}^2}$,
解得$x=\frac{1}{3}$,即$\overrightarrow{AE}=\frac{1}{3}\overrightarrow{AB}$,
再设$\overrightarrow{AF}=y\overrightarrow{AC}$,y∈[0,1],
∴$\overrightarrow{AF}•\overrightarrow{EF}=\overrightarrow{AF}•(\overrightarrow{AF}-\overrightarrow{AE})={\overrightarrow{AF}^2}-\overrightarrow{AF}•\overrightarrow{AE}$=${y^2}{\overrightarrow{AC}^2}-y\overrightarrow{AC}•\frac{1}{3}\overrightarrow{AB}=16{y^2}-y(\overrightarrow{AB}+\overrightarrow{AD})•\frac{1}{3}\overrightarrow{AB}$=$16{y^2}-\frac{y}{3}{\overrightarrow{AB}^2}-\frac{y}{3}\overrightarrow{AD}•\overrightarrow{AB}=16{y^2}-\frac{7}{2}y=16{(y-\frac{7}{64})^2}-\frac{49}{256}$.
显然y∈[0,1],当$y=\frac{7}{64}$时,$\overrightarrow{AF}•\overrightarrow{EF}$有最小值为$-\frac{49}{256}$.
点评 本题考查了平面向量的基本定理,平面向量的数量积运算,属于中档题.


科目:高中数学 来源: 题型:解答题
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
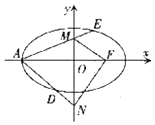 已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.
已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com