
【题目】已知数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,且满足
,且满足 ![]() ,求数列
,求数列 ![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() ,
, ![]() ,
, ![]() .
.
猜想: ![]() .
.
然后用数学归纳法证明.证明过程如下:
①当 ![]() 时, , 猜想成立
时, , 猜想成立
②假设 ![]() (
( ![]() N*)时,猜想成立,即
N*)时,猜想成立,即 ![]() .
.
那么,当 ![]() 时,由已知
时,由已知 ![]() ,得
,得 ![]() .
.
又 ![]() ,两式相减并化简,得
,两式相减并化简,得 ![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
所以,当 ![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何 ![]() N*都成立.
N*都成立.
思路2:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() .
.
由已知 ![]() ,写出
,写出 ![]() 与
与 ![]() 的关系式:
的关系式: ![]() ,
,
两式相减,得 ![]() 与
与 ![]() 的递推关系式:
的递推关系式: ![]() .
.
整理: ![]() .
.
发现:数列 ![]() 是首项为 , 公比为的等比数列.
是首项为 , 公比为的等比数列.
得出:数列 ![]() 的通项公式
的通项公式 ![]() , 进而得到
, 进而得到 ![]() .
.
【答案】["![]() ","
","![]() ","
","![]() ","
","![]() ","
","![]() ","
","![]() ","
","![]() ","
","![]() ","
","![]() ","
","![]() 【解析】思路1.由于
【解析】思路1.由于 ![]() ,令
,令 ![]() ,可求出
,可求出 ![]() 的值,再令
的值,再令 ![]() ,可求出
,可求出 ![]() 的值,再令
的值,再令 ![]() ,可求出
,可求出 ![]() 的值,利用不完全归纳法,归纳猜想出
的值,利用不完全归纳法,归纳猜想出 ![]() ,再用数学归纳法加以证明, 这是一种“归纳—猜想—证明”思维方式,从特殊到一般的归纳推理方式;思路2.采用构造法直接求出数列得通项公式.
,再用数学归纳法加以证明, 这是一种“归纳—猜想—证明”思维方式,从特殊到一般的归纳推理方式;思路2.采用构造法直接求出数列得通项公式.
试题解析:思路1.由于 ![]() ,令
,令 ![]() ,
, ![]() ;令
;令 ![]() ,
, ![]() ,
, ![]() ,令
,令 ![]() ,
, ![]() ,则
,则
![]() ,由此猜想
,由此猜想 ![]() ;下面用数学归纳法证明,证明过程如下:
;下面用数学归纳法证明,证明过程如下:
①当 ![]() 时,
时, ![]() ,得
,得 ![]() ,符合
,符合 ![]() ,猜想成立.
,猜想成立.
②假设 ![]() (
( ![]() N*)时,猜想成立,即
N*)时,猜想成立,即 ![]() ,
,
那么,当 ![]() 时,由已知
时,由已知 ![]() ,得
,得 ![]()
![]() ,
, ![]()
又 ![]() ,两式相减并化简,得
,两式相减并化简,得 ![]() ,
, ![]()
![]() (用含
(用含 ![]() 的代数式表示).所以,当
的代数式表示).所以,当 ![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何 ![]() N*都成立.
N*都成立.
思路2. 先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() ,
,
由已知 ![]() ,写出
,写出 ![]() 与
与 ![]() 的关系式:
的关系式: ![]() ,
,
两式相减,得 ![]() 与
与 ![]() 的递推关系式:
的递推关系式: ![]() ,
,
整理: ![]()
![]() ,
, ![]()
发现:数列 ![]() 是首项为2,公比为2的等比数列.
是首项为2,公比为2的等比数列.
得出:数列 ![]() 的通项公式
的通项公式 ![]()
![]() ,进而得到
,进而得到 ![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】在2015﹣2016赛季CBA联赛中,某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表(注:表中分数 ![]() ,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根据统计表的信息:
(1)从上述比赛中等可能随机选择一场,求甲球员在该场比赛中投篮命中率大于0.5的概率;
(2)试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率;
(3)在接下来的3场比赛中,用X表示这3场比赛中乙球员命中率超过0.5的场次,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
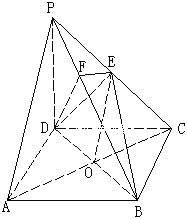
(1)证明:PA∥平面EDB
(2)证明:平面BDE![]() 平面PCB
平面PCB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面 ![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在 ![]() 和
和 ![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在 ![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos2x﹣sin2x的图象向左平移 ![]() 个单位后得到函数F(x)的图象,则下列说法正确的是( )
个单位后得到函数F(x)的图象,则下列说法正确的是( )
A.函数F(x)是奇函数,最小值是 ![]()
B.函数F(x)是偶函数,最小值是 ![]()
C.函数F(x)是奇函数,最小值是﹣2
D.函数F(x)是偶函数,最小值是﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足① ![]() =
= ![]() ,②直线AQ与BP的交点在椭圆E:
,②直线AQ与BP的交点在椭圆E: ![]() +
+ ![]() =1(a>b>0)上.
=1(a>b>0)上.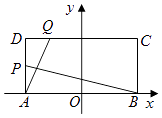
(Ⅰ)求椭圆E的方程;
(Ⅱ)设R为椭圆E的右顶点,M为椭圆E第一象限部分上一点,作MN垂直于y轴,垂足为N,求梯形ORMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com