
【题目】已知函数f(x)=lnx﹣ ![]() ax2+x,a∈R.
ax2+x,a∈R.
(1)若f(1)=0,求函数f(x)的最大值;
(2)令g(x)=f(x)﹣(ax﹣1),求函数g(x)的单调区间;
(3)若a=﹣2,正实数x1 , x2满足f(x1)+f(x2)+x1x2=0,证明x1+x2≥ ![]() .
.
【答案】
(1)解:因为f(1)= ![]() ,所以a=2.
,所以a=2.
此时f(x)=lnx﹣x2+x,x>0,
![]() ,
,
由f'(x)=0,得x=1,所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故当x=1时函数有极大值,也是最大值,所以f(x)的最大值为f(1)=0.
(2)解: ![]() ,
,
所以 ![]() .
.
当a≤0时,因为x>0,所以g′(x)>0.
所以g(x)在(0,+∞)上是递增函数,
当a>0时, ![]() ,
,
令g′(x)=0,得 ![]() .
.
所以当 ![]() 时,g′(x)>0;当
时,g′(x)>0;当 ![]() 时,g′(x)<0,
时,g′(x)<0,
因此函数g(x)在 ![]() 是增函数,在
是增函数,在 ![]() 是减函数.
是减函数.
综上,当a≤0时,函数g(x)的递增区间是(0,+∞),无递减区间;
当a>0时,函数g(x)的递增区间是 ![]() ,递减区间是
,递减区间是 ![]() .
.
(3)解:由x1>0,x2>0,即x1+x2>0.
令t=x1x2,则由x1>0,x2>0得, ![]() .t>0
.t>0
可知,φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.
所以φ(t)≥φ(1)=1,
所以 ![]() ,解得
,解得 ![]() 或
或 ![]() .
.
又因为x1>0,x2>0,
因此 ![]() 成立.
成立.
【解析】(1)先求出a的值,然后求原函数的极值即可;(2)求导数,然后通过研究不等式的解集确定原函数的单调性;(3)结合已知条件构造函数,然后结合函数单调性得到要证的结论.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() +
+ ![]() =1(a>b>0)的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,O为坐标原点:
=1(a>b>0)的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,O为坐标原点: 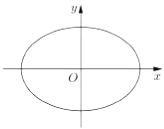
(1)求椭圆Г的方程:
(2)设点A在椭圆Г上,点B在直线y=2上,且OA⊥OB,求证: ![]() +
+ ![]() 为定值:
为定值:
(3)设点C在Γ上运动,OC⊥OD,且点O到直线CD距离为常数d(0<d<2),求动点D的轨迹方程:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. 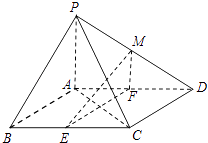
(1)求证:EF⊥平面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,sin2B=2sinAsinC.
(1)若a=b,求cosB的值;
(2)若B=60°,△ABC的面积为4 ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD= ![]() ,F是PB中点,E为BC上一点.
,F是PB中点,E为BC上一点. 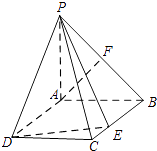
(1)求证:AF⊥平面PBC;
(2)当BE为何值时,二面角C﹣PE﹣D为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=![]() ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com