
【题目】如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F. 
(1)求证:ACBC=ADAE;
(2)若AF=2,CF=2 ![]() ,求AE的长.
,求AE的长.
【答案】
(1)证明:如图所示,连接BE.
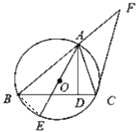
∵AE是⊙O的直径,∴∠ABE=90°.
又∠E与∠ACB都是 ![]() 所对的圆周角,
所对的圆周角,
∴∠E=∠ACB.
∵AD⊥BC,∠ADC=90°.
∴△ABE∽△ADC,
∴AB:AD=AE:AC,
∴ABAC=ADAE.
又AB=BC,
∴BCAC=ADAE.
(2)解:∵CF是⊙O的切线,
∴CF2=AFBF,
∵AF=2,CF=2 ![]() ,
,
∴(2 ![]() )2=2BF,解得BF=4.
)2=2BF,解得BF=4.
∴AB=BF﹣AF=2.
∵∠ACF=∠FBC,∠CFB=∠AFC,
∴△AFC∽△CFB,
∴AF:FC=AC:BC,
∴AC= ![]() =
= ![]() .
.
∴cos∠ACD= ![]() ,
,
∴sin∠ACD= ![]() =sin∠AEB,
=sin∠AEB,
∴AE= ![]() =
= ![]()
【解析】(1)如图所示,连接BE.由于AE是⊙O的直径,可得∠ABE=90°.利用∠E与∠ACB都是 ![]() 所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(2)利用切割线定理可得CF2=AFBF,可得BF.再利用△AFC∽△CFB,可得AF:FC=AC:BC,进而根据sin∠ACD=sin∠AEB,AE=
所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(2)利用切割线定理可得CF2=AFBF,可得BF.再利用△AFC∽△CFB,可得AF:FC=AC:BC,进而根据sin∠ACD=sin∠AEB,AE= ![]() ,即可得出答案.
,即可得出答案.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了很大的便利,但也给城市的管理带来了一些困难,现某城市为了解人们对“共享单车”投放的认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 赞成投放的人数 | 赞成投放的人数占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|
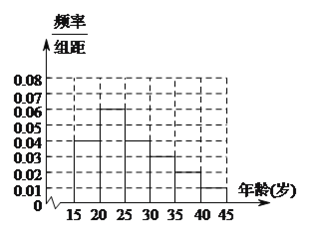
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取
)在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取![]() 人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
(![]() )在(
)在(![]() )中抽取的
)中抽取的![]() 人中随机选派
人中随机选派![]() 人作为领队,求所选派的
人作为领队,求所选派的![]() 人中第五组至少有一人的概率.
人中第五组至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在斜率为2的直线![]() ,使得当直线
,使得当直线![]() 与椭圆
与椭圆![]() 有两个不同交点
有两个不同交点![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
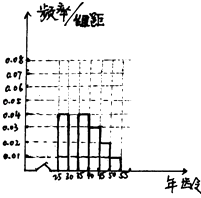
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)当实数![]() 变化时,求
变化时,求![]() 的最大值;
的最大值;
(3)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com