
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有两个不同的实数解
有两个不同的实数解![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 在
在![]() 单调递减.(2)证明见解析;
单调递减.(2)证明见解析;
【解析】
(1)求出函数的导数,通过讨论![]() 的范围求出函数的单调区间即可;
的范围求出函数的单调区间即可;
(2)求出函数的导数,通过讨论![]() 的范围求出函数的单调区间,结合函数的单调性证明即可.
的范围求出函数的单调区间,结合函数的单调性证明即可.
解:函数![]() 的定义域是
的定义域是![]() ,
,
![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递减.
单调递减.
(2)证明:设![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
所以![]() 在
在![]() 处取得最大值.
处取得最大值.
当![]() 时,方程
时,方程![]() 有两个不同的实数解
有两个不同的实数解![]() ,
,![]()
所以函数![]() 的两个不同的零点
的两个不同的零点![]() ,
,![]() ,一个零点比1小,一个零点比1大.
,一个零点比1小,一个零点比1大.
不妨设![]() ,
,
由![]() ,且
,且![]() ,得
,得![]() ,且
,且![]() ,
,
则![]() ,所以
,所以![]() ,
,
所以![]() ,令
,令![]() ,
,![]() ,
,
![]() .
.![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.30C.35D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 和等比数列
和等比数列![]() 中,
中, ![]() ,
,![]() ,
,![]() 是
是![]() 前
前![]() 项和.
项和.
(1)若 ![]() ,求实数
,求实数![]() 的值;
的值;
(2)是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中?若存在,求出所有的
中?若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数![]() ,使得数列
,使得数列![]() 中至少有三项在数列
中至少有三项在数列![]() 中,但
中,但![]() 中的项不都在数列
中的项不都在数列![]() 中?若存在,求出一个可能的
中?若存在,求出一个可能的![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 是椭圆内任一点.设经过
是椭圆内任一点.设经过![]() 的两条不同直线
的两条不同直线![]() 分别于椭圆交于点
分别于椭圆交于点![]() 记
记![]() 的斜率分别为
的斜率分别为![]()
(1)当![]() 经过椭圆右焦点且
经过椭圆右焦点且![]() 为
为![]() 中点时,求:
中点时,求:
①椭圆![]() 的标准方程;
的标准方程;
②四边形![]() 面积
面积![]() 的取值范围.
的取值范围.
(2)当![]() 时,若点
时,若点![]() 重合于点
重合于点![]()
![]() ,且
,且![]() .求证:直线
.求证:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.如图是2015—2019年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误的是( )
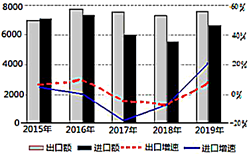
A.这五年,出口总额之和比进口总额之和大
B.这五年,2015年出口额最少
C.这五年,2019年进口增速最快
D.这五年,出口增速前四年逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: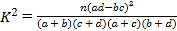 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,如图,曲线
,如图,曲线![]() 由曲线
由曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
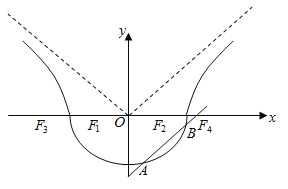
(Ⅰ)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+a2+…+an=an+1﹣2.
(1)若a1=2,求数列{an}的通项公式;
(2)若数列1,a2,a4,b1,b2,…bn,…成等差数列,求数列{bn}的前n项和为Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com