
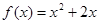 .
.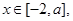 求
求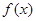 的值域;
的值域;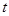 ,当
,当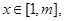
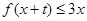 恒成立,求实数
恒成立,求实数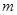 的取值范围.
的取值范围.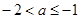 时,
时, 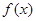 的值域为:
的值域为: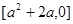 .当
.当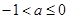 时,
时,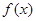 的值域为:
的值域为: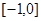 .当
.当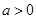 时,
时,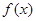 的值域为:
的值域为: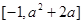 .(II)
.(II)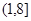 .
.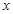 的范围含有参数
的范围含有参数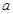 ,故结合抛物线的图象对
,故结合抛物线的图象对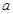 分情况进行讨论.
分情况进行讨论. 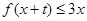 恒成立得:
恒成立得: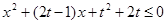 恒成立,
恒成立,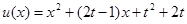 ,
,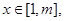 则只需
则只需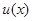 的最大值小于等于0.
的最大值小于等于0.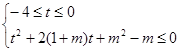 ,令
,令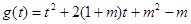
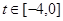 ,使得
,使得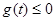 .这又需要
.这又需要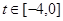 时
时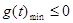 .接下来又对二次函数
.接下来又对二次函数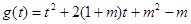 分情况讨论,从而求出实数
分情况讨论,从而求出实数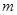 的取值范围.
的取值范围.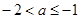 时,
时,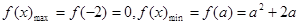 ,
,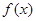 的值域为:
的值域为: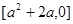 2分
2分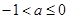 时,
时,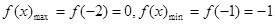 ,
,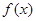 的值域为:
的值域为: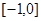 4分
4分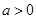 时,
时,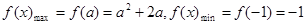 ,
,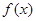 的值域为:
的值域为: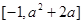 6分
6分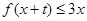 恒成立得:
恒成立得: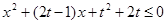 恒成立,
恒成立,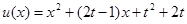 ,
,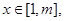 因为抛物线的开口向上,所以
因为抛物线的开口向上,所以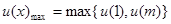 ,由
,由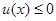 恒成立知:
恒成立知: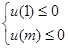 8分
8分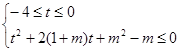 令
令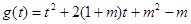
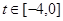 ,使得
,使得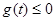 即:当
即:当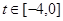 ,
,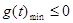 10分
10分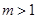 ,
,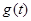 的对称轴:
的对称轴: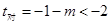
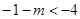 即:
即: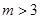 时,
时,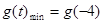

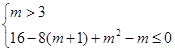 解得:
解得: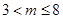
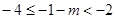 即:
即: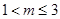 时,
时,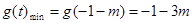

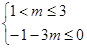 解得:
解得: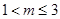
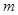 的取值范围为:
的取值范围为: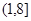 13分
13分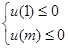 ,
,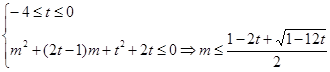 有解.
有解.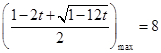 ,则
,则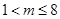 .
.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com