
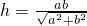 ;现在把结论类比到空间:三棱锥S-ABC的三条侧棱SA,SB,SC两两相互垂直,SH⊥平面ABC,且SA=a,SB=b,SC=c,则点S到平面ABC的距离h'=________.
;现在把结论类比到空间:三棱锥S-ABC的三条侧棱SA,SB,SC两两相互垂直,SH⊥平面ABC,且SA=a,SB=b,SC=c,则点S到平面ABC的距离h'=________.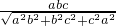
 ,SM=
,SM=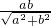 ,同理在直角三角形CSM中可求得|CM|=
,同理在直角三角形CSM中可求得|CM|=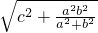 ,于是S△ABC=
,于是S△ABC= •|AB|•|CM|=
•|AB|•|CM|= •
• •
•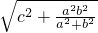 =
= •
•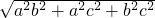 ,由VS-ABC=VC-ABS,即可求得S到平面ABC的距离为h′.
,由VS-ABC=VC-ABS,即可求得S到平面ABC的距离为h′.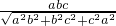 .
. ,又ab=|AB|•|SM|
,又ab=|AB|•|SM|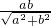 ,
,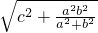 ,
, •|AB|•|CM|=
•|AB|•|CM|= •
• •
•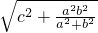 =
= •
•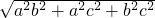 ,
, •
• abc=
abc= S△ABC•h′=
S△ABC•h′= •
• •
•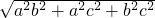 •h′,
•h′,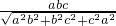 ,
,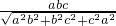 .
.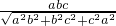 .
.

科目:高中数学 来源: 题型:
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com