【题目】一批产品中,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样的方法,从这批产品中抽取一个容量为20的样本,写出抽样过程,并说明采用哪种抽样方法更能反映总体水平.
【答案】见解析
【解析】试题分析：系统抽样方法, 将200件产品用随机方式编号,并分成20个组,每组10个产品,用抽签的方法从第一组中抽取一个产品,再依次加抽样间距,这样就得到容量为20的一个样本.
试题解析：
系统抽样方法:
将200件产品用随机方式编号,并分成20个组,每组10个产品,用抽签的方法从第一组中抽取一个产品,再依次加抽样间距,这样就得到容量为20的一个样本.
分层抽样方法:
∵一、二、三级品的个数比为5∶3∶2,
∴需要从一级品中抽取
×20=10(个),二级品中抽取
×20=6(个),三级品中抽取
×20=4(个).
将一级品的100个产品按00,01,…,99编号,将二级品的60个产品按00,01,…,59编号;将三级品的40个产品按00,01,…,39编号,采用随机数表法,分别从中抽取10个、6个、4个,这样就得到一个容量为20的样本.此题中采用分层抽样更好,样本更能反映总体的各类水平.
浙江名校名师金卷系列答案
全优冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】设等差数列
的前
项和为
，在同一个坐标系中，
及
的部分图象如图所示，则（ ）．
A. 当
时，取得最大值 B. 当
时，取得最大值
C. 当时，取得最小值 D. 当时，取得最小值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】.某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图所示的频率分布直方图.
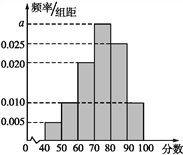
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的学生人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a＞0，b＞0，且a2+b2= 
，若a+b≤m恒成立，
（Ⅰ）求m的最小值；
（Ⅱ）若2|x﹣1|+|x|≥a+b对任意的a，b恒成立，求实数x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如表的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
（1）试求y关于x的回归直线方程；（参考公式： 
= 
， 
=y﹣ 
）
（2）已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元，根据（1）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润L（x）最大？（利润=售价﹣收购价）
查看答案和解析>>
科目：高中数学 来源： 题型：
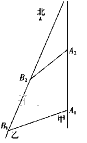
【题目】如图，甲船以每小时30
海里的速度向正北方向航行，乙船按固定方向匀速直线航行．当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，此时两船相距20海里．当甲船航行20分钟到达A2处时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10海里，问乙船每小时航行多少海里？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
