解:(Ⅰ)证明:∵x
n+1-(λ+1)x
n+λx
n-1=0(n∈N
*且n≥2),λ为非零常数,
∴x
n+1-x
n=λ(x
n-x
n-1),
∵x
1=a,x
2=b,其中a、b为常数,且a<b,
∴x
2-x
1=b-a>0,
∴数列{x
n+1-x
n}是首项为b-a,公比为λ的等比数列,
故
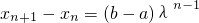
,
∵λ>0,
∴x
n+1-x
n>0,
即x
n+1>x
n(n∈N
*).
(Ⅱ)∵x
1=a,x
2=b,x
n+1-(λ+1)x
n+λx
n-1=0(n∈N
*且n≥2),
其中a、b为常数,且a<b,λ为非零常数.
∴x
n+1-λx
n=x
n-λx
n-1=…=x
2-λx
1=b-λa,
即x
n+1-λx
n=b-λa,
∴λx
n=x
n+1-(b-λa),①
∵x
n+1>x
n(n∈N
*),
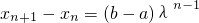
,
∴
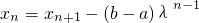
,②
②-①,得(1-λ)x
n=b-λa-(b-a)•λ
n-1,
∴
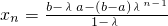
,
∵|λ|<1,
∴
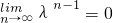
,
∴
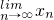
=
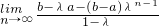
=
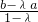
.
分析:(Ⅰ)由题设得x
n+1-x
n=λ(x
n-x
n-1),由x
2-x
1=b-a>0,知:数列{x
n+1-x
n}是首项为b-a,公比为λ的等比数列,由此能够证明x
n+1>x
n(n∈N
*).
(Ⅱ)由x
n+1-λx
n=x
n-λx
n-1=…=x
2-λx
1=b-λa及x
n+1>x
n(n∈N
*),知
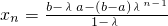
,由|λ|<1,知
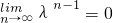
,由此能求出
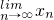
.
点评:本题考查数列与不等式的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,是高考的重点.解题时要认真审题,注意极限的灵活运用.

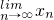 .
.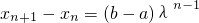 ,
,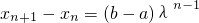 ,
,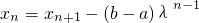 ,②
,②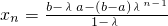 ,
,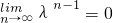 ,
,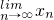 =
=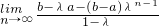 =
=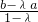 .
.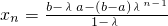 ,由|λ|<1,知
,由|λ|<1,知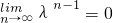 ,由此能求出
,由此能求出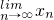 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案