
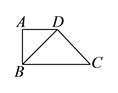
【题目】如图所示,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,构成四面体
,构成四面体![]() ,则在四面体
,则在四面体![]() 中,下列说法不正确的是( ).
中,下列说法不正确的是( ).
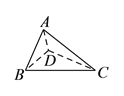
A. 直线![]() 直线
直线![]() B. 直线
B. 直线![]() 直线
直线![]()
C. 直线![]() 平面
平面![]() D. 平面
D. 平面![]() 平面
平面![]()
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|.
(1)若点P的轨迹为曲线![]() ,求此曲线的方程;
,求此曲线的方程;
(2)若点Q在直线l1: x+y+3=0上,直线l2经过点Q且与曲线![]() 只有一个公共点M,求|QM|的最小值.
只有一个公共点M,求|QM|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域均为
的定义域均为![]() ,且
,且![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求![]() 的解析式,并证明:当
的解析式,并证明:当![]() 时,
时,![]() ;
;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最高点为M(
,且图象上一个最高点为M( ![]() ,3).
,3).
(1)求f(x)的解析式;
(2)先把函数y=f(x)的图象向左平移 ![]() 个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,试写出函数y=g(x)的解析式.
个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,试写出函数y=g(x)的解析式.
(3)在(2)的条件下,若总存在x0∈[﹣ ![]() ,
, ![]() ],使得不等式g(x0)+2≤log3m成立,求实数m的最小值.
],使得不等式g(x0)+2≤log3m成立,求实数m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4cos2x﹣4 ![]() sinxcosx的最小正周期为π(>0).
sinxcosx的最小正周期为π(>0).
(1)求的值;
(2)若f(x)的定义域为[﹣ ![]() ,
, ![]() ],求f(x)的最大值与最小值及相应的x的值.
],求f(x)的最大值与最小值及相应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+)(ω>0,0≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π.
(1)求f(x)的解析式;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知从全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表:若按![]() 的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10号的概率.

附: 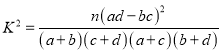

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 交于
交于![]() ,设
,设![]() ,
, ![]() ,给出以下四个命题:
,给出以下四个命题:
①![]()
②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小;
的面积最小;
③四边形![]() 周长
周长![]() ,
, ![]() ,则
,则![]() 是奇函数;
是奇函数;
④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com