
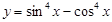 的最小正周期是
的最小正周期是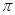
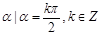 }
}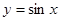 的图象和函数y=x的图象有三个公共点
的图象和函数y=x的图象有三个公共点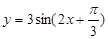 的图象向右平移
的图象向右平移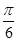 得到
得到 的图象
的图象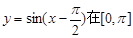 上是减函数
上是减函数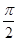 ,k∈Z};故②不正确;
,k∈Z};故②不正确;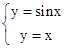 得sinx=x,令g(x)=x-sinx,g′(x)=1-cosx≥0,
得sinx=x,令g(x)=x-sinx,g′(x)=1-cosx≥0,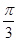 )的图象向右平移
)的图象向右平移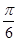 得到y=3sin[2(x-
得到y=3sin[2(x-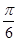 )+
)+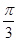 ]=3sin2x,故④正确;
]=3sin2x,故④正确;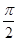 )=-cosx在(0,π)上是增函数,故⑤不正确.故答案为①④。
)=-cosx在(0,π)上是增函数,故⑤不正确.故答案为①④。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com