
【题目】某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为![]() ,如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组
,如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组![]() 的人数为4人.
的人数为4人.
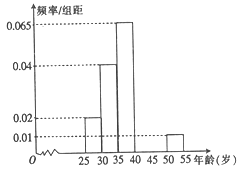
(1)求第五组的频率并估计200名志愿者中年龄在40岁以上(含40岁)的人数;
(2)若从年龄位于第四组和第六组的志愿者中随机抽取两名,记他们的年龄分别为![]() ,事件
,事件![]() ,求
,求![]() .
.
【答案】(1)75(2)![]()
【解析】试题分析:(1)由频率分布直方图,小长方形面积对应对应区间的概率,从而所有小长方形面积和为1,因此先根据频率等于频数除以总数求出第四组的频率,再利用补集思想求第五组的频率,而年龄在40岁以上(含40岁)的人为后三组人数之和,先求出后三组频率,再根据频数等于总数与频率乘积得所求人数;(2)先根据频数等于总数与频率乘积得第四组![]() 第六组人数,利用枚举法确定抽取的两名的总事件数,满足
第六组人数,利用枚举法确定抽取的两名的总事件数,满足![]() 等价抽取的两名志愿者在同一组,再由枚举法确定事件数,最后根据古典概型概率公式求概率.
等价抽取的两名志愿者在同一组,再由枚举法确定事件数,最后根据古典概型概率公式求概率.
试题解析:(1)第四组的频率为![]() ,所以第五组的频率为
,所以第五组的频率为![]() ,由直方图得后三组频率为
,由直方图得后三组频率为![]()
所以200名志愿者中年龄在40岁以上(含40岁)的人数约为![]() 人.
人.
(2)第四组![]() 的人数为4人,设为
的人数为4人,设为![]() ;第六组
;第六组![]() 的人数为2人,设为
的人数为2人,设为![]() .则有
.则有
![]() 共15种情况,
共15种情况,
因事件![]() 发生当且仅当随机抽取的两名志愿者在同一组,所以事件
发生当且仅当随机抽取的两名志愿者在同一组,所以事件![]() 包含的基本事件为
包含的基本事件为![]() 共 7 种情况,故
共 7 种情况,故![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点在
的焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的左顶点为
的左顶点为![]() ,斜率为
,斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(Ⅰ)当点![]() 为椭圆的上顶点,
为椭圆的上顶点, ![]() 的面积为
的面积为![]() 时,求椭圆的离心率;
时,求椭圆的离心率;
(Ⅱ)当![]() ,
, ![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),将
为参数),将![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 和
和![]() 倍后得到曲线
倍后得到曲线![]() .以平面直角坐标系
.以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)试写出曲线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小,并求此最小值.
的距离最小,并求此最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖。抽奖规则如下:1、抽奖方案有以下两种:方案![]() ,从装有1个红球、2个白球(仅颜色不同)的甲袋中随机摸出1个球,若是红球,则获得奖金15元,否则,没有奖金,兑奖后将摸出的球放回甲袋中;方案
,从装有1个红球、2个白球(仅颜色不同)的甲袋中随机摸出1个球,若是红球,则获得奖金15元,否则,没有奖金,兑奖后将摸出的球放回甲袋中;方案![]() ,从装有2个红、1个白球(仅颜色不同)的乙袋中随机摸出1个球,若是红球,则获得奖金10元,否则,没有奖金,兑奖后将摸出的球放回乙袋中。
,从装有2个红、1个白球(仅颜色不同)的乙袋中随机摸出1个球,若是红球,则获得奖金10元,否则,没有奖金,兑奖后将摸出的球放回乙袋中。
抽奖条件是:顾客购买商品的金额满100元,可根据方案![]() 抽奖一;满足150元,可根据方案
抽奖一;满足150元,可根据方案![]() 抽奖(例如某顾客购买商品的金额为310元,则该顾客采用的抽奖方式可以有以下三种,根据方案
抽奖(例如某顾客购买商品的金额为310元,则该顾客采用的抽奖方式可以有以下三种,根据方案![]() 抽奖三次或方案
抽奖三次或方案![]() 抽奖两次或方案
抽奖两次或方案![]() 各抽奖一次)。已知顾客
各抽奖一次)。已知顾客![]() 在该商场购买商品的金额为250元。
在该商场购买商品的金额为250元。
(1)若顾客![]() 只选择根据方案
只选择根据方案![]() 进行抽奖,求其所获奖金为15元的概率;
进行抽奖,求其所获奖金为15元的概率;
(2)当若顾客![]() 采用每种抽奖方式的可能性都相等,求其最有可能获得的奖金数(0元除外)。
采用每种抽奖方式的可能性都相等,求其最有可能获得的奖金数(0元除外)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com