
ЁОЬтФПЁПЭМ1ЪЧФГИпМмЧХЯфСКЕФКсНиУцЃЌЫќгЩЩЯВПТЗУцКЭЯТВПжЇГХЯфСНВПЗжзщГЩЃЎШчЭМ2ЃЌТЗУцПэЖШ![]() ЃЌЯТВПжЇГХЯфCDEFЮЊЕШбќЬнаЮЃЈ
ЃЌЯТВПжЇГХЯфCDEFЮЊЕШбќЬнаЮЃЈ![]() ЃЉЃЌЧв
ЃЉЃЌЧв![]() ЃЎЮЊСЫБЃжЄГажиФмСІгыЮШЖЈадЃЌашЯТВПжЇГХЯфЕФУцЛ§ЮЊ
ЃЎЮЊСЫБЃжЄГажиФмСІгыЮШЖЈадЃЌашЯТВПжЇГХЯфЕФУцЛ§ЮЊ![]() ЃЌИпЖШЮЊ2mЧв
ЃЌИпЖШЮЊ2mЧв![]() ЃЌШєТЗУцABЃЎВрБпCFКЭDEЃЌЕзВПEFЕФдьМлЗжБ№ЮЊ4aЧЇдЊ/mЃЌ5aЧЇдЊ/mЃЌ6aЧЇдЊ/mЃЈaЮЊе§ГЃЪ§ЃЉЃЌ
ЃЌШєТЗУцABЃЎВрБпCFКЭDEЃЌЕзВПEFЕФдьМлЗжБ№ЮЊ4aЧЇдЊ/mЃЌ5aЧЇдЊ/mЃЌ6aЧЇдЊ/mЃЈaЮЊе§ГЃЪ§ЃЉЃЌ![]() ЃЎ
ЃЎ

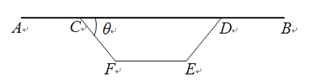
ЃЈ1ЃЉЪдгУІШБэЪОЯфСКЕФзмдьМлyЃЈЧЇдЊЃЉЃЛ
ЃЈ2ЃЉЪдШЗЖЈcosІШЕФжЕЃЌЪЙзмдьМлзюЕЭ?ВЂЧѓзюЕЭзмдьМлЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() ЪБЃЌзмдьМлзюЕЭЃЌЮЊ
ЪБЃЌзмдьМлзюЕЭЃЌЮЊ![]() ЧЇдЊЃЎ
ЧЇдЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуFзї![]() гкЕуHЃЌгЩШ§НЧКЏЪ§МАжЇГХУцУцЛ§ПЩЕУ
гкЕуHЃЌгЩШ§НЧКЏЪ§МАжЇГХУцУцЛ§ПЩЕУ![]() ЃЌаДГізмдьМлгыІШЕФЙиЯЕЃЌВЂЗжЮіКЏЪ§ЖЈвхгђЃЛ
ЃЌаДГізмдьМлгыІШЕФЙиЯЕЃЌВЂЗжЮіКЏЪ§ЖЈвхгђЃЛ
ЃЈ2ЃЉРћгУЕМЪ§ЧѓКЏЪ§ЕФзюаЁжЕЃЌМДПЩЕУЕННсТл.
ЃЈ1ЃЉЙ§ЕуFзї![]() гкЕуHЃЌдђ
гкЕуHЃЌдђ![]() ЃЌ
ЃЌ
Ыљвддк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Щш![]() ЃЌ
ЃЌ
дђгЩЬтвтЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
ЙЪТЗУцABЕФдьМлЮЊ![]() ЧЇдЊЃЌ
ЧЇдЊЃЌ
ВрБпCFКЭDEЕФдьМлЮЊ![]() ЧЇдЊЃЎ
ЧЇдЊЃЎ
ЕзВПEFЕФдьМлЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
гжвђЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
ЩшШёНЧ![]() Тњзу
Тњзу![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
вђДЫЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊ![]()
Щш![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ
дђ![]() ЃЎ
ЃЎ
Сю![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
вђЮЊ![]() ЃЎ
ЃЎ
Ыљвд![]() ЃЌСаБэШчЯТЃК
ЃЌСаБэШчЯТЃК
|
|
|
|
|
|
| Ѓ | 0 | ЃЋ | ||
| 4 |
ЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌга
ЃЌга![]() ЃЎ
ЃЎ
Д№ЃКЕБ![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() ЪБЃЌзмдьМлзюЕЭЃЌЮЊ
ЪБЃЌзмдьМлзюЕЭЃЌЮЊ![]() ЧЇдЊЃЎ
ЧЇдЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉвбжЊЪ§Са![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌЧвЪ§Са
ЃЌЧвЪ§Са![]() ЮЊЕШБШЪ§СаЃЌЧѓГЃЪ§pЃЛ
ЮЊЕШБШЪ§СаЃЌЧѓГЃЪ§pЃЛ
ЃЈ2ЃЉЩш![]() ЁЂ
ЁЂ![]() ЪЧЙЋБШВЛЯрЕШЕФСНИіЕШБШЪ§СаЃЌ
ЪЧЙЋБШВЛЯрЕШЕФСНИіЕШБШЪ§СаЃЌ![]() ЃЌжЄУїЃКЪ§Са
ЃЌжЄУїЃКЪ§Са![]() ВЛЪЧЕШБШЪ§Са.
ВЛЪЧЕШБШЪ§Са.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() ЃЌ
ЃЌ![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЩЯЕФСНИіЖЏЕуЃЌ
ЩЯЕФСНИіЖЏЕуЃЌ![]() ЪЧзјБъдЕуЃЌЯђСП
ЪЧзјБъдЕуЃЌЯђСП![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() .ЩшдВ
.ЩшдВ![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉжЄУїЯпЖЮ![]() ЪЧдВ
ЪЧдВ![]() ЕФжБОЖЃЛ
ЕФжБОЖЃЛ
ЃЈ2ЃЉЕБдВ![]() ЕФдВаФЕНжБЯп
ЕФдВаФЕНжБЯп![]() ЕФОрРыЕФзюаЁжЕЮЊ
ЕФОрРыЕФзюаЁжЕЮЊ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯжбиЖдНЧЯп
ЃЌЯжбиЖдНЧЯп![]() НЋ
НЋ![]() елЦ№ЃЌЪЙЕуAЕНДяЕуPЃЌЕуMЃЌNЗжБ№дкжБЯп
елЦ№ЃЌЪЙЕуAЕНДяЕуPЃЌЕуMЃЌNЗжБ№дкжБЯп![]() ЃЌ
ЃЌ![]() ЩЯЃЌЧвAЃЌBЃЌMЃЌNЫФЕуЙВУц.
ЩЯЃЌЧвAЃЌBЃЌMЃЌNЫФЕуЙВУц.
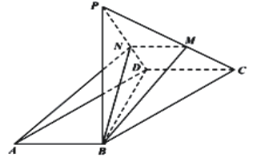
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЖўУцНЧ
ЃЌЖўУцНЧ![]() ЦНУцНЧДѓаЁЮЊ
ЦНУцНЧДѓаЁЮЊ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНax2+2axЉlnxЉ1ЃЌaЁЪRЃЎ
ЃЈ1ЃЉЕБa![]() ЪБЃЌЧѓfЃЈxЃЉЕФЕЅЕїЧјМфМАМЋжЕЃЛ
ЪБЃЌЧѓfЃЈxЃЉЕФЕЅЕїЧјМфМАМЋжЕЃЛ
ЃЈ2ЃЉШєaЮЊећЪ§ЃЌЧвВЛЕШЪНfЃЈxЃЉЁнxЖдШЮвтxЁЪЃЈ0ЃЌ+ЁоЃЉКуГЩСЂЃЌЧѓaЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() КЭ
КЭ![]() Тњзу
Тњзу![]() Шє
Шє![]() ЮЊЕШБШЪ§СаЃЌЧв
ЮЊЕШБШЪ§СаЃЌЧв![]()
ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌМЧЪ§Са
ЃЌМЧЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]()
ЂйЧѓ![]() ЃЛ
ЃЛ
ЂкЧѓе§ећЪ§ kЃЌЪЙЕУЖдШЮвт![]() Ољга
Ољга![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧѓЯТСаИїЪНМЋЯоЃК
ЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ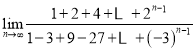 ЃЛ
ЃЛ
ЃЈ3ЃЉ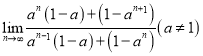 ЃЛ
ЃЛ
ЃЈ4ЃЉ![]() ЃЛ
ЃЛ
ЃЈ5ЃЉ![]() ЃЛ
ЃЛ
ЃЈ6ЃЉ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФЦцЪ§ЯюЪЧЪзЯюЮЊ1ЕФЕШВюЪ§СаЃЌХМЪ§ЯюЪЧЪзЯюЮЊ2ЕФЕШБШЪ§Са.Ъ§Са
ЕФЦцЪ§ЯюЪЧЪзЯюЮЊ1ЕФЕШВюЪ§СаЃЌХМЪ§ЯюЪЧЪзЯюЮЊ2ЕФЕШБШЪ§Са.Ъ§Са![]() ЧА
ЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЧвТњзу
ЃЌЧвТњзу![]()
ЃЈ1ЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЧѓЪ§Са![]() ЧА
ЧА![]() ЯюКЭ
ЯюКЭ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдкЪ§Са![]() жаЃЌЪЧЗёДцдкСЌајЕФШ§Яю
жаЃЌЪЧЗёДцдкСЌајЕФШ§Яю![]() ЃЌАДдРДЕФЫГађГЩЕШВюЪ§СаЃПШєДцдкЃЌЧѓГіЫљгаТњзуЬѕМўЕФе§ећЪ§
ЃЌАДдРДЕФЫГађГЩЕШВюЪ§СаЃПШєДцдкЃЌЧѓГіЫљгаТњзуЬѕМўЕФе§ећЪ§![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§Ртжљ![]() жаЃЌ
жаЃЌ![]() ЦНУц
ЦНУц![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊСтаЮЃЎ
ЮЊСтаЮЃЎ
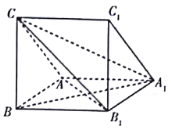
ЃЈЂёЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЖўУцНЧ
ЃЌЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ЃЌЧѓШ§РтзЖ
ЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЎ
ЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com