
【题目】某人在静水中游泳,速度为4![]() 公里/小时,他在水流速度为4公里/小时的河中游泳.
公里/小时,他在水流速度为4公里/小时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
【答案】解:(1)如左图,设人游泳的速度为![]() ,水流的速度为
,水流的速度为![]() ,以
,以![]() 、
、![]() 为邻边作平行四边形OACB,则此人的实际速度为
为邻边作平行四边形OACB,则此人的实际速度为![]() +
+![]() =
=![]()
由勾股定理知|![]() |=8
|=8
且在Rt△ACO中,∠COA=60°,
故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8公里/小时.
(2)如右图,设此人的实际速度为![]() ,水流速度为
,水流速度为![]() ,则游速为
,则游速为![]() =
=![]() ﹣
﹣![]() ,
,
在Rt△AOD中,|![]() |=4
|=4![]() ,|
,|![]() |=4,|
|=4,|![]() |=4
|=4![]() ,cos∠DAO=
,cos∠DAO= ![]()
∴∠DAO=arccos![]() .
.
故此人沿与河岸成arccos![]() 的夹角逆着水流方向前进,实际前进的速度大小为4
的夹角逆着水流方向前进,实际前进的速度大小为4![]() 公里/小时.
公里/小时.
【解析】(1)如左图,设人游泳的速度为![]() , 水流的速度为
, 水流的速度为![]() , 以
, 以![]() 、
、![]() 为邻边作平行四边形OACB,则此人的实际速度为
为邻边作平行四边形OACB,则此人的实际速度为![]() +
+![]() =
=![]() , 可得结论;
, 可得结论;
(2)如右图,设此人的实际速度为 ![]() , 水流速度为
, 水流速度为![]() , 则游速为
, 则游速为 ![]() =
=![]() ﹣
﹣![]() , 可得结论.
, 可得结论.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)
)∪(1,+∞)
B.( ![]() ,1)
,1)
C.( ![]() )
)
D.(﹣∞,﹣ ![]() ,)
,) ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() (
(![]() ),从
),从![]() 上的点
上的点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,再从点
,再从点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() .设
.设![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: 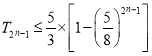 ;
;
(Ⅲ)若已知![]() (
(![]() ),记数列
),记数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(Ⅰ)证明:CD⊥AE;
(Ⅱ)证明:PD⊥平面ABE;
(Ⅲ)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0,另一边CD所在直线方程为x+3y+7=0,
(Ⅰ)求正方形中心G所在的直线方程;
(Ⅱ)设正方形中心G(x0 , y0),当正方形仅有两个顶点在第一象限时,求x0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°.
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,B= ![]() ,AC=2
,AC=2 ![]() ,cosC=
,cosC= ![]() .
. 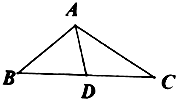
(1)求sin∠BAC的值及BC的长度;
(2)设BC的中点为D,求中线AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com