
����Ŀ����96�죨������ȫ���Ǿ���Ʒ������2017��3��23����25�����Ĵ��ٰ�.չ�ݸ���һ�Ҵ�����ɫ����Ϊ���о��λ������뱾������ԭ���������Ĺ�ϵ���ڽ���ǰ���������5�ν���IJλ�����![]() �����ˣ����������ԭ��������
�����ˣ����������ԭ��������![]() ���������õ��������ݣ�
���������õ��������ݣ�

��������������������ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
�������õ�����ԭ����12������Ϥ���ν����Լ��13���˲μӣ�Ϊ�˱�֤ԭ�����ܹ�������Ҫ����õ�Ӧ�����ٲ���ԭ���϶��ٴ���
���ο���ʽ��  ��
�� ![]() ��
��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����������ͼ�����ڲ����������������ֵΪ�� ��
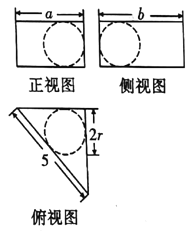
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0��a��1������f��x��=loga��x+1����![]() �� ��F��x��=2f��x��+g��x��
�� ��F��x��=2f��x��+g��x��
��1������F��x���Ķ�����D������㣻
��2��������x�ķ���F��x����m=0������[0��1�����н⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+4ax+2a+6��
��1��������f��x��=log2 f��x������СֵΪ2����a��ֵ��
��2����������x��R������f��x����0����������g��a��=2��a|a+3|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijӡˢ��Ϊ���о�ӡˢ�����鼮�ijɱ�![]() ����λ��Ԫ����ӡˢ����
����λ��Ԫ����ӡˢ����![]() ����λ��ǧ�ᣩ֮��Ĺ�ϵ����ӡ��ij���鼮ʱ������ͳ�ƣ�������ݼ��±���
����λ��ǧ�ᣩ֮��Ĺ�ϵ����ӡ��ij���鼮ʱ������ͳ�ƣ�������ݼ��±���
ӡˢ���� | 2 | 3 | 4 | 5 | 8 |
����ɱ� | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
�����������ݣ�������Ա�ֱ�����ס������ֲ�ͬ�Ļع�ģ�ͣ��õ������ع鷽�̣����̼ף� ![]() �������ң�
�������ң� ![]() .
.
��1��Ϊ����������ģ�͵����Ч���������������.
������±�����������ȷ��0.1����
ӡˢ���� | 2 | 3 | 4 | 5 | 8 | |
����ɱ� | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ģ�ͼ� | ����ֵ | 2.4 | 2.1 | 1.6 | ||
�в� | 0 | -0.1 | 0.1 | |||
ģ���� | ����ֵ | 2.3 | 2 | 1.9 | ||
�в� | 0.1 | 0 | 0 | |||
�ڷֱ����ģ�ͼ���ģ���ҵIJв�ƽ����![]() ��
��![]() ����ͨ���Ƚ�
����ͨ���Ƚ�![]() ��
�� ![]() �Ĵ�С���ж��ĸ�ģ�����Ч������.
�Ĵ�С���ж��ĸ�ģ�����Ч������.
��2����������֮���ܵ����������һ�ӭ�����ñ�ȫ������������ӡˢ���������ж���ӡˢ.�����г����飬��������Ϊ8ǧ�ᣨ����0.8����10ǧ�ᣨ����0.2������ӡˢ����ÿ��5Ԫ�ļ۸��鼮���۸������̣���ӡˢ������ӡˢ8ǧ�ỹ��10ǧ���ܻ�ø�����������1�������Ч���Ϻõ�ģ�ͼ���ӡˢ������ijɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ǿռ���A�е�Ԫ�ظ����ã�A����ʾ�����壨A��B��= ![]() ����A={��1��0}��B={x||x2��2x��3|=a}���ң�A��B����1����a�����п���ֵΪ�� ��
����A={��1��0}��B={x||x2��2x��3|=a}���ң�A��B����1����a�����п���ֵΪ�� ��
A.{a|a��4}
B.{a|a��4��a=0}
C.{a|0��a��4}
D.{a|a��4��a=0}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�ĵ���ABCD�Ǿ��Σ�ƽ��PAB��ƽ��ABCD��PA=AB=3��BC=2��E��F�ֱ�����AD��PC���е� 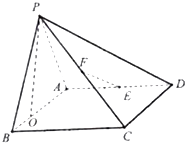
��1����֤��EF��ƽ��PBC
��2����ֱ��PC��ƽ��ABCD���ɽ�Ϊ ![]() ����P��AB�ϵ���ӰO�ڿ�����B��һ�࣬������P��EF��A������ֵ��
����P��AB�ϵ���ӰO�ڿ�����B��һ�࣬������P��EF��A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ��x+1��2+y2=25��Բ��ΪC��A��1��0����Բ��һ���㣬QΪԲ������һ�㣮�߶�AQ�Ĵ�ֱƽ������CQ�����߽��ڵ�M����M�Ĺ켣����Ϊ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ,
, ![]() ��������
��������![]() ��,Բ
��,Բ![]() ��ԭ������
��ԭ������![]() ��������.
��������.
(��) ��![]() �ķ��̣�
�ķ��̣�
(��) ��![]() ,��
,��![]() ����
����![]() ���غϣ���ֱ��
���غϣ���ֱ��![]() ���˶�,����
���˶�,����![]() ��
��![]() ����������,�е�ֱ�Ϊ
����������,�е�ֱ�Ϊ![]() ,
, ![]() .��֤��
.��֤�� ![]() ������
������![]() Ϊ����ԭ�㣩.
Ϊ����ԭ�㣩.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com