
【题目】已知![]() 是椭圆
是椭圆![]() 上的两点.
上的两点.
(1)求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于另一点
交于另一点![]() (不同于点
(不同于点![]() ),若以
),若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将A和B点的坐标代入椭圆G的方程,列出方程组求出![]() 的值,再求出
的值,再求出![]() 和离心率;
和离心率;
(2)由(1)求出椭圆G的方程,对直线![]() 的斜率进行讨论,不妨设直线
的斜率进行讨论,不妨设直线![]() 的方程,与椭圆G的方程联立后,利用韦达定理写出式子,将条件转化为
的方程,与椭圆G的方程联立后,利用韦达定理写出式子,将条件转化为![]() ,由向量数量积的坐标运算列出式子,代入化简后求出
,由向量数量积的坐标运算列出式子,代入化简后求出![]() 的值,即得直线
的值,即得直线![]() 的方程.
的方程.
解:(1)由已知![]() ,
,
由点![]() 在椭圆
在椭圆![]() 上可得
上可得![]() ,
,
解得![]() .
.
所以![]() ,
,
所以椭圆![]() 的离心率是
的离心率是![]() ;
;
(2)当直线![]() 过点
过点![]() 且斜率不存在时,可得点
且斜率不存在时,可得点![]() ,不满足条件;
,不满足条件;
设直线![]() 的方程为
的方程为![]() ),点
),点![]() ,
,
由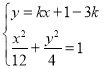 可得
可得![]() ,
,
显然![]() ,此方程两个根是点
,此方程两个根是点![]() 和点
和点![]() 的橫坐标,
的橫坐标,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
因为以![]() 为直径的圆经过点
为直径的圆经过点![]() ,
,
所以![]() ,即
,即![]() ,
,
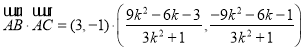
![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,即直线
时,即直线![]() ,与已知点
,与已知点![]() 不同于点
不同于点![]() 矛盾,
矛盾,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】2018年,某地认真贯彻落实中央十九大精神和各项宏观调控政策,经济运行平稳增长,民生保障持续加强,惠民富民成效显著,城镇居民收入稳步增长,收入结构稳中趋优.据当地统计局公布的数据,现将8月份至12月份当地的人均月收入增长率与人均月收入分别绘制成折线图(如图一)与不完整的条形统计图(如图二).请从图中提取相关的信息:
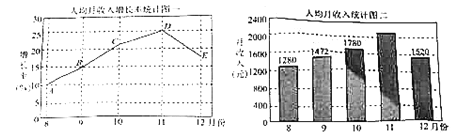
①10月份人均月收入增长率为![]() 左右;
左右;
②11月份人均月收入为2047元;
③从上图可知该地9月份至12月份人均月收入比8月份人均月收入均得到提高.
其中正确的信息个数为( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比为 q的等比数列,且a1,a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 引圆
引圆![]() 的两条切线
的两条切线![]() ,切线
,切线![]() 与抛物线
与抛物线![]() 的另一交点分别为
的另一交点分别为![]() ,线段
,线段![]() 中点的横坐标记为
中点的横坐标记为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
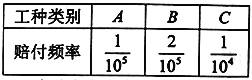
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com