
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)设出等比数列的公比q,由![]() ,利用等比数列的通项公式化简后得到关于q的方程,由已知等比数列的各项都为正数,得到满足题意q的值,然后再根据等比数列的通项公式化简
,利用等比数列的通项公式化简后得到关于q的方程,由已知等比数列的各项都为正数,得到满足题意q的值,然后再根据等比数列的通项公式化简![]() ,把求出的q的值代入即可求出等比数列的首项,根据首项和求出的公比q写出数列的通项公式即可;(Ⅱ)把(Ⅰ)求出数列{an}的通项公式代入设bn=log3a1+log3a2+…+log3an,利用对数的运算性质及等差数列的前n项和的公式化简后,即可得到bn的通项公式,求出倒数即为
,把求出的q的值代入即可求出等比数列的首项,根据首项和求出的公比q写出数列的通项公式即可;(Ⅱ)把(Ⅰ)求出数列{an}的通项公式代入设bn=log3a1+log3a2+…+log3an,利用对数的运算性质及等差数列的前n项和的公式化简后,即可得到bn的通项公式,求出倒数即为![]() 的通项公式,然后根据数列的通项公式列举出数列的各项,抵消后即可得到数列{
的通项公式,然后根据数列的通项公式列举出数列的各项,抵消后即可得到数列{![]() }的前n项和
}的前n项和
试题解析:(Ⅰ)设数列{an}的公比为q,由![]() =9a2a6得
=9a2a6得![]() =9
=9![]() ,所以q2=
,所以q2=![]() .
.
由条件可知q>0,故q=![]() .由2a1+3a2=1得2a1+3a1q=1,所以a1=
.由2a1+3a2=1得2a1+3a1q=1,所以a1=![]() .
.
故数列{an}的通项公式为an=![]() .
.
(Ⅱ)bn=log3a1+log3a2+…+log3an=-(1+2+…+n)=-![]() .
.
故![]() .
.
![]()
所以数列![]() 的前n项和为
的前n项和为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C:x2+y2+4x﹣2y+m=0与直线x﹣ ![]() y+
y+ ![]() ﹣2=0相切.
﹣2=0相切.
(1)求圆C的方程;
(2)若圆C上有两点M,N关于直线x+2y=0对称,且|MN|=2 ![]() ,求直线MN的方程.
,求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
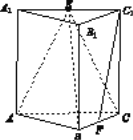
【题目】如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,AB⊥BC, ![]() ,
,
E,F分别是A1C1,BC的中点.
(Ⅰ)求证:C1F∥平面ABE;
(Ⅱ)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 2 | 4 | 8 | 4 | 2 |
男生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 1 | 5 | 6 | 5 | 3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
男生 | |||
女生 | |||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,向量m=(2b,1),n=(2a-c,cos C),且m∥n.(1)若b2=ac,试判断△ABC的形状;(2)求y=1-![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x﹣sinxcosx
(1)求f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
(3)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
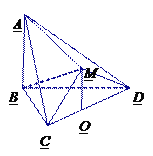
【题目】如图,在多面体![]() 中,△
中,△![]() 是等边三角形,△
是等边三角形,△![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1) 求证: ![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com