练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

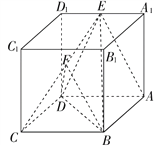
    【题目】如图，正方体ABCD－A1B1C1D1中，点E是A1D1的中点，点F是CE的中点．

    (Ⅰ)求证：平面ACE⊥平面BDD1B1；

    (Ⅱ)求证：AE∥平面BDF.

    【答案】(1)见解析(2)见解析

    【解析】试题分析：（Ⅰ）通过证明AC⊥平面BDD1B1，即可证明平面ACE⊥平面BDD1B1；

    （Ⅱ）通过证明OF∥AE，即可证明AE∥平面BDF．

    试题解析：

    (Ⅰ)在正方体中，ABCD是正方形，BB1⊥平面ABCD，

    ∴AC⊥BD，AC⊥BB1，

    ∵BD∩BB1＝B，BD，

    BB1平面BDD1B1，

    ∴AC⊥平面BDD1B1，

    ∵AC平面ACE，∴平面ACE⊥平面BDD1B1.6分

    (Ⅱ)连AC交BD于G，连FG，

    ∵ABCD是正方形，∴G是AC中点，

    ∵F是CE是中点，∴AE∥FG，

    ∵AE平面BDF，FG平面BDF，

    ∴AE∥平面BDF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中， ， ， ， 分别是的中点.

    （1）求证： 平面；

    （2）求平面与平面所成的锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R的函数是偶函数，且满足上的解析式为，过点作斜率为k的直线l，若直线l与函数的图象至少有4个公共点，则实数k的取值范围是

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线.

    (1)求曲线在点P(2,4)处的切线方程；

    (2)求曲线过点P(2,4)的切线方程；

    (3)求斜率为1的曲线的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： 的离心率为，右焦点为F，上顶点为A，且△AOF的面积为 (O为坐标原点).

    (1)求椭圆C的方程；

    (2)设P是椭圆C上的一点，过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M，证明：|PF|＋|PM|为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(导学号：05856290)[选修4－5：不等式选讲]

    已知函数f(x)＝|x－a|＋|x－2a|.

    (Ⅰ)对任意x∈R，不等式f(x)>1成立，求实数a的取值范围；

    (Ⅱ)当a＝－1时，解不等式f(x)<3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝emx＋x2－mx.

    (1)证明：f(x)在(－∞，0)单调递减，在(0，＋∞)单调递增；

    (2)若对于任意x1，x2∈[－1,1]，都有，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品按质量标准分为,,,,五个等级.现从一批该产品随机抽取20个，对其等级进行统计分析，得到频率分布表如下：

    等级

    频率

    （1）在抽取的20个产品中，等级为5的恰有2个，求,；

    （2）在（1）的条件下，从等级为3和5的所有产品中，任意抽取2个，求抽取的2个产品等级恰好相同的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求曲线在点处的切线方程;

    （2）令，讨论的单调性并判断有无极值，若有，求出极值.

    查看答案和解析>>

    同步练习册答案