
分析 (1)利用条件,两边平方,利用基本不等式,即可证得结论;
(2)分析使不等式$\sqrt{x-1}$+$\sqrt{x-4}$<$\sqrt{x-2}$+$\sqrt{x-3}$成立的充分条件,一直分析到使不等式成立的充分条件显然具备,从而不等式得证.
解答 证明:∵a+b+c=1,
∴1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≤3(a2+b2+c2),
∴a2+b2+c2≥$\frac{1}{3}$.
(2)当x≥4时,要证$\sqrt{x-1}$+$\sqrt{x-4}$<$\sqrt{x-2}$+$\sqrt{x-3}$,
两边平方只需证$\sqrt{(x-1)(x-4)}<\sqrt{(x-2)(x-3)}$,
只需证x2-5x+6>x2-5x+4,
即证6>4,
显然上式成立,
所以原不等式成立,即$\sqrt{x-1}$+$\sqrt{x-4}$<$\sqrt{x-2}$+$\sqrt{x-3}$.
点评 本题考查不等式的证明,考查基本不等式的运用,考查利用分析法证明不等式,利用用分析法证明不等式的关键是寻找使不等式成立的充分条件,直到使不等式成立的充分条件已经显然具备为止,属于中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ②③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{10}{3}$] | B. | [2,$\frac{10}{3}$] | C. | (2,+∞) | D. | [$\frac{10}{3}$,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
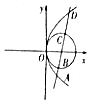 如图,抛物线C1:y2=2x和圆C2:(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$,其中p>0,直线l经过C1的焦点,依次交C1,C2于A,B,C,D四点,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值为$\frac{1}{4}$.
如图,抛物线C1:y2=2x和圆C2:(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$,其中p>0,直线l经过C1的焦点,依次交C1,C2于A,B,C,D四点,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com