
����Ŀ�����к�ɨ�ڡ��ڳ�������������ά������ȶ��ͺ�ƽ��չ.ɨ�ڳ����ڼ䣬����Υ����������Ͷ����ij�й������ض�ij������7������Ͷ������Ա������ͳ�ƣ�![]() ��ʾ��
��ʾ��![]() ������Ͷ�����������õ�ͳ�Ʊ������£�
������Ͷ�����������õ�ͳ�Ʊ������£�
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
��1����![]() ��
��![]() ����������ع�ϵ��������ϱ��ṩ�����ݣ�����С���˷����
����������ع�ϵ��������ϱ��ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2�������![]() ��
��![]() ֮��������ػ��Ǹ����.��д����ȷ�𰸣�����˵�����ɣ�
֮��������ػ��Ǹ����.��д����ȷ�𰸣�����˵�����ɣ�
��3��Ԥ��ڰ��������Ͷ��������������������ȡ��������.
�ο���ʽ��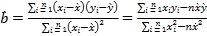 ��
�� ![]() ./span>
./span>

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ֱ�Ϊ˫����
�ֱ�Ϊ˫����![]() �����ҽ��㣬MΪ˫������֧��һ��������
�����ҽ��㣬MΪ˫������֧��һ��������![]() ����ֱ��
����ֱ��![]() ��˫���ߵ���һ������ΪN����
��˫���ߵ���һ������ΪN����![]() �����Ϊ__________.
�����Ϊ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��Բ����һ���ڽӵȱ�Բ����һ��������Բ�ĵ����ϣ���������������ε�Բ���������ڵȱ�Բ�����ϵ���صõ�СԲ����һ���ڽӵȱ�Բ����������������ȥ.
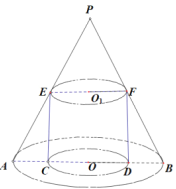
��1��֤����Щ�ȱ�Բ��������Ӵ�С�ų�һ���ȱ����У�
��2����֪��Щ�ȱ�Բ�������֮��Ϊԭ��Բ�����![]() �������ĵȱ�Բ���������Բ�����֮��.
�������ĵȱ�Բ���������Բ�����֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ABCD��A1B1C1D1�dz����壬O��B1D1���е㣬ֱ��A1C��ƽ��AB1D1�ڵ�M�������н�����ȷ��( )

A.A��M��O���㹲��B.A��M��O��A1������
C.A��M��C��O������D.B��B1��O��M����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı߳�Ϊ2��
�ı߳�Ϊ2��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ����
����![]() ��λ�ã�ʹƽ��
��λ�ã�ʹƽ��![]() ƽ��
ƽ��![]() ��
��
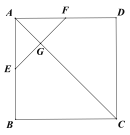

������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
����������![]() ������ֵ��
������ֵ��
�����ж��߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ
��ʹ![]() ƽ��
ƽ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ������
Ϊ������![]() �Ľ��㣬����
�Ľ��㣬����![]() ��ֱ��
��ֱ��![]() ��������
��������![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ��������
��������![]() ��
��![]() ���㴦�����߷ֱ���
���㴦�����߷ֱ���![]() ����
����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .��
.��![]() ����
����![]() ��ֵ��___�������
��ֵ��___�������![]() ��ʾ��.
��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y2��2px��p��0���Ľ���F��ֱ���������߽���A��B���㣬��![]() 3
3![]() �������ߵ���l��x�ύ���C��AA1��ֱl�ڵ�A1�����ı���AA1CF�����Ϊ
�������ߵ���l��x�ύ���C��AA1��ֱl�ڵ�A1�����ı���AA1CF�����Ϊ![]() ������l�ķ���Ϊ�� ��
������l�ķ���Ϊ�� ��
A.![]() B.
B.![]() C.x����2D.x����1
C.x����2D.x����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() �������������γɵ����������Ϊ
�������������γɵ����������Ϊ![]() .��
.��
��1����֤������![]() Ϊ��ʵ����ֱ��
Ϊ��ʵ����ֱ��![]() ������P��
������P��
��2���ֱ���![]() ��
��![]() ʱ������Ӧ��ֱ��������
ʱ������Ӧ��ֱ��������
��3�����![]() �IJ�ͬȡֵ�����ۼ���
�IJ�ͬȡֵ�����ۼ���![]() ֱ��
ֱ��![]() ����P������������Χ�ɵ����������Ϊ
����P������������Χ�ɵ����������Ϊ![]() �е�Ԫ�ظ���.
�е�Ԫ�ظ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ұ߳����ͼ���㷨˼·Դ���ҹ��Ŵ���ѧ�����������������еġ������������. ִ�иó����ͼ���������![]() �ֱ�Ϊ16,20���������
�ֱ�Ϊ16,20���������![]() �� ��
�� ��

A. 0B. 2C. 4D. 1
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com