
分析 (Ⅰ)问题转化为f(x)min≤0,求出函数的导数,得到函数的最小值,从而求出a的范围即可;
(Ⅱ)令a=1,则f(x)=x-ln(x+1),问题转化为证明em-n-1>m-n即可,记 g(x)=ex-x-1,(x>0),根据函数的单调性证明即可.
解答 解:(Ⅰ)关于x的不等式f(x)≤0有实数解,即f(x)min≤0…(1分)
∵$f'(x)=1-\frac{1}{x+1}=\frac{x}{x+1}$,(x>-1),由 f'(x)<0⇒-1<x<0
∴f(x)在(-1,0]递减,在[0,+∞)递增,$f{(x)_{min}}=f(0)=\frac{a-1}{a}$…(4分)
由 $\frac{a-1}{a}≤0$得 0<a≤1,∴a的取值范围为(0,1]…(5分)
(Ⅱ)令a=1,则f(x)=x-ln(x+1),由(Ⅰ)知f(x)在[0,+∞)递增,
∵m>n>0,∴f(m)>f(n)即 m-ln(m+1)>n-ln(n+1)…(7分)
∴m-n>ln(m+1)-ln(n+1),故要证原不等式,只要证:em-n-1>m-n…(9分)
记 g(x)=ex-x-1,(x>0),则 g'(x)=ex-1>0…(10分)
∴g(x)在(0,+∞)递增,∴g(x)>g(0)=0即 ex-1>x(x>0)
令x=m-n,则有:em-n-1>m-n,∴em-n-1>ln(m+1)-ln(n+1)…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:解答题
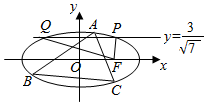 已知右焦点为F的椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)与直线y=$\frac{3}{\sqrt{7}}$相交于P,Q两点,且PF⊥QF.
已知右焦点为F的椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)与直线y=$\frac{3}{\sqrt{7}}$相交于P,Q两点,且PF⊥QF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在矩形ABCD中,AB=5,BC=2,现截去一个△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x∈(0,2],CQ=t.
在矩形ABCD中,AB=5,BC=2,现截去一个△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x∈(0,2],CQ=t.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 从气球A上测得正前方的河流的两岸B,C的俯角分别为α,β,如果这时气球的高是100米,则河流的宽度BC为( )
从气球A上测得正前方的河流的两岸B,C的俯角分别为α,β,如果这时气球的高是100米,则河流的宽度BC为( )| A. | $\frac{100(tanβ-tanα)}{tanαtanβ}$ | B. | $\frac{100tanαtanβ}{tanα-tanβ}$ | ||
| C. | $\frac{100(tanα+tanβ)}{tanαtanβ}$ | D. | $\frac{100tanαtanβ}{tanα+tanβ}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4$\sqrt{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | 8$\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,0) | C. | [1,3) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com