
【题目】新疆在种植棉花有着得天独厚的自然条件,土质呈碱性,夏季温差大,阳光充足,光合作用充分,生长时间长,这种环境下种植的棉花绒长品质好产量髙,所以新疆棉花举世闻名.每年五月份,新疆地区进入灾害天气高发期,灾害天数对当年棉花产量有着重要影响,根据过去五年的数据统计,得到相关数据如下表:
灾害天气天数 | 2 | 3 | 4 | 5 | 8 |
棉花产量 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,技术人员分别借助甲乙两种不同的回归模型,得到两个回归方程,
方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:① 完成下表;(计算结果精确到0.1)
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并比铰
,并比铰![]() 的大小,判断哪个模型拟合效果更好?
的大小,判断哪个模型拟合效果更好?
灾害天气天数 | 2 | 3 | 4 | 5 | 8 | |
棉花产量 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 |
| 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
(2)根据天气预报,今年五月份新疆![]() 市灾害天气是6天的概率是0.5,灾害天气是7天的概率为0.4,灾害天气是10天的概率为0.1,若何女士在新疆
市灾害天气是6天的概率是0.5,灾害天气是7天的概率为0.4,灾害天气是10天的概率为0.1,若何女士在新疆![]() 市承包了15公顷地种植棉花,请你根据第(1)问中拟合效果较好的模型估计一下何女士今年棉花的产量.(计算过程中所有结果精确到0.01)
市承包了15公顷地种植棉花,请你根据第(1)问中拟合效果较好的模型估计一下何女士今年棉花的产量.(计算过程中所有结果精确到0.01)
【答案】(1)①表格见解析②见解析(2)![]() 吨
吨
【解析】
(1)根据已知模型计算,然后计算残差平方和,小的效果好;
(2)利用模型2估算出灾害天气为6,7,10时的棉花产量![]() ,得
,得![]() 分布列,由期望公式计算期望后可得.
分布列,由期望公式计算期望后可得.
(1)①完成表格如下:
灾害天气天数 | 2 | 3 | 4 | 5 | 8 | |
棉花产量 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 3.1 | 2.4 | 2.1 | 1.9 | 1.6 |
残差 | 0.1 | 0 |
| 0 | 0.1 | |
模型乙 | 估计值 | 3.2 | 2.3 | 2 | 1.9 | 1.7 |
残差 | 0 | 0.1 | 0 | 0 | 0 | |
②计算模型甲的残差平方和为![]() ,
,
模型乙的残差平方和为![]() ,
,
∴![]() ,模型乙的拟合效果更好.
,模型乙的拟合效果更好.
(2)设今年棉花的单位产量为![]() 吨公顷,则
吨公顷,则![]() 的分布列如下表:
的分布列如下表:
| 1.78 | 1.73 | 1.66 |
| 0.5 | 0.4 | 0.1 |
于是![]() ,所以何女士今年棉花的产量大约是
,所以何女士今年棉花的产量大约是![]() 吨
吨


科目:高中数学 来源: 题型:
【题目】用细钢管焊接而成的花坛围栏构件如图所示,它的外框是一个等腰梯形PQRS,内部是一段抛物线和一根横梁,抛物线的顶点与梯形上底中点是焊接点O,梯形的腰紧靠在抛物线上,两条腰的中点是梯形的腰、抛物线以及横梁的焊接点A,B,抛物线与梯形下底的两个焊接点为C,D,已知梯形的高是40厘米,C,D两点间的距离为40厘米.
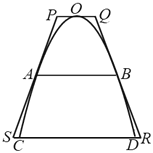
(1)求横梁AB的长度;
(2)求梯形外框的用料长度;
(注:细钢管的粗细等因素忽略不计,结果精确到1厘米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国昂首阔步地走进2019年,迎来了她70岁华诞.某平台组织了“伟大的复兴之路一新中国70周年知识问答”活动,规则如下:共有30道单选题,每题4个选项中只有一个正确,每答对一题获得5颗红星,每答错一题反扣2颗红星;若放弃此题,则红星数无变化.答题所获得的红星可用来兑换神秘礼品,红星数越多奖品等级越高.小强参加该活动,其中有些题目会做,有些题目可以排除若干错误选项,其余的题目则完全不会.
(1)请问:对于完全不会的题目,小强应该随机从4个选项中选一个作答,还是选择放弃?(利用统计知识说明理由)
(2)若小强有12道题目会做,剩下的题目中,可以排除一个错误选项、可以排除两个错误选项和完全不会的题目的数量比是![]() .请问:小强在本次活动中可以获得最多红星数的期望是多少?
.请问:小强在本次活动中可以获得最多红星数的期望是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生![]() 人,编号为
人,编号为![]() ,
,![]() ,…,
,…,![]() ;女生
;女生![]() 人,编号为
人,编号为![]() ,
,![]() ,…,
,…,![]() .为了解学生的学习状态,按编号采用系统抽样的方法从这
.为了解学生的学习状态,按编号采用系统抽样的方法从这![]() 名学生中抽取
名学生中抽取![]() 人进行问卷调查,第一组抽到的号码为
人进行问卷调查,第一组抽到的号码为![]() ,现从这
,现从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人进行座谈,则这
人进行座谈,则这![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为
的最小值为![]() ,
,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象关于原点对称.
的图象关于原点对称.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com