【题目】如图，在四棱柱ABCD-A1B1C1D1中，已知平面AA1C1C⊥平面ABCD，且AB=BC=CA=
，AD=CD=1.
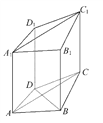
(1)求证：BD⊥AA1.
(2)在棱BC上取一点E，使得AE∥平面DCC1D1，求
的值.
【答案】（1）见解析（2）1
【解析】(1)在四边形ABCD中，因为BA=BC，DA=DC，所以BD⊥AC，平面AA1C1C⊥平面ABCD，且平面ACC1A1∩平面ABCD=AC，BD平面ABCD，所以BD⊥平面ACC1A1，又AA1平面ACC1A1，所以BD⊥AA1.
(2)点E为BC的中点，即
=1，
下面给予证明：在三角形ABC中，因为AB=AC，且E为BC的中点，所以AE⊥BC，又在四边形ABCD中，AB=BC=CA=
，DA=DC=1，所以∠ACB=60°，∠ACD=30°，所以DC⊥BC，即平面ABCD中有AE∥DC.因为DC平面DCC1D1，AE平面DCC1D1，所以AE∥平面DCC1D1.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】设某单位用2160万元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房．经测算，如果将楼房建为x（x≥10）层，则每平方米的平均建筑费用为560＋48x（单位：元）．
（1）写出楼房平均综合费用y关于建造层数x的函数关系式；
（2）该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？
（注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用/建筑总面积）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，函数
.
（1）若
的定义域为
，求实数
的取值范围；
（2）当
时，求函数
的最小值
；
（3）是否存在非负实数
，使得函数
的定义域为
，值域为
，若存在，求出
的值；若不存在，则说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
的参数方程为
（
为参数），曲线
的参数方程为
（
为参数），在以
为极点，
轴的正半轴为极轴的极坐标系中，射线
，与
，
各有一个交点，当
时，这两个交点间的距离为2，当
，这两个交点重合．
（1）分别说明，是什么曲线，并求出
与
的值；
（2）设当
时，
与，的交点分别为
，当
，
与，的交点分别为
，求四边形
的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某厂有4台大型机器，在一个月中，一台机器至多出现1次故障，且每台机器是否出现故障是相互独立的，出现故障时需1名工人进行维修，每台机器出现故障需要维修的概率为
.
(1)若出现故障的机器台数为
，求
的分布列；
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%？
(3)已知一名工人每月只有维修1台机器的能力，每月需支付给每位工人1万元的工资，每台机器不出现故障或出现故障能及时维修，就使该厂产生5万元的利润，否则将不产生利润，若该厂现有2名工人，求该厂每月获利的均值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在梯形
中， 
， 
， 
，四边形
为矩形，平面
平面
， 
．
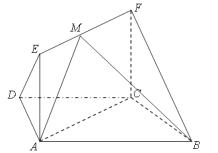
（1）求证： 
平面
；
（2）点
在线段
上运动，设平面
与平面
所成二面角的平面角为
，试求
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
