Question

【题目】如图，四边形是平行四边形，平面，，，，，，，为的中点.

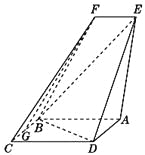
（1）求证：平面；

（2）求证：平面平面；

（3）求多面体的体积.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）.

【解析】试题分析：（1）证明线面平行可证明直线平行于平面内的直线，本题中只需证明；（2）证明面面垂直可证明其中一个平面经过另外一个平面的垂线，本题中只需证明平面中的平面；（3）不规则多面体的体积求解时将其分割为柱体和椎体分别求体积

试题解析：（1）证明：如图，取的中点，连接，，

在中，∵是的中点，

∴且，又∵，∴且，即四边形是平行四边形，∴．又平面，平面，∴平面．

（2）证明：在中，，取中点，连，∵，

∴，又，∴，∴，

∴，又平面，平面，∴，∵，

∴平面．又∵平面，∴平面平面．

（3）解：连，并延长交于，连．

∵分别为的中点，∴，∴是中点，∵，，

∴多面体为三棱柱，体积为，且四边形为平行四边形，∴，∵平面，∴平面，四棱锥的体积为，

∴多面体的体积为．