
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:

计算说明哪位运动员的成绩更稳定.
【答案】(1)![]() (2)乙
(2)乙
【解析】试题分析:(1)求出从6人中随机选出2人,选出的2人中至少有1个女运动员的基本事件数,计算对应的概率值;
(2)根据题目中茎叶图的数据,计算甲、乙运动员的平均成绩与方差,比较大小即可得出结论.
试题解析:
(1)把4个男运动员和2个女运动员分别记为a1,a2,a3,a4和b1,b2.
则基本事件包括(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2)共15种.
其中至少有1个女运动员的情况有9种,
故至少有1个女运动员的概率P=![]() =
=![]() .
.
(2)设甲运动员的平均成绩为![]() 甲,方差为s
甲,方差为s![]() ,乙运动员的平均成绩为
,乙运动员的平均成绩为![]() 乙,方差为s
乙,方差为s![]() ,
,
可得![]() 甲=
甲=![]() =71,
=71,![]() 乙=
乙=![]() =71,
=71,
s![]() =
=![]() [(68-71)2+(70-71)2+(71-71)2+(72-71)2+(74-71)2]=4,
[(68-71)2+(70-71)2+(71-71)2+(72-71)2+(74-71)2]=4,
s![]() =
=![]() [(69-71)2+(70-71)2+(70-71)2+(72-71)2+(74-71)2]=3.2.
[(69-71)2+(70-71)2+(70-71)2+(72-71)2+(74-71)2]=3.2.
因为![]() 甲=
甲=![]() 乙,s
乙,s![]() >s
>s![]() ,故乙运动员的成绩更稳定.
,故乙运动员的成绩更稳定.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).
编 号 | 分 组 | 频 数 |
1 | [0,2) | 12 |
2 | [2,4) | 16 |
3 | [4,6) | 34 |
4 | [6,8) | 44 |
续 表
编 号 | 分 组 | 频 数 |
5 | [8,10) | 50 |
6 | [10,12) | 24 |
7 | [12,14) | 12 |
8 | [14,16) | 4 |
9 | [16,18] | 4 |
合计 | 200 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况为:5,6,7,8,9,10.把这6名学生的得分看成一个总体.
(1)求该总体的平均数;
(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·湖北武汉第二次调研)如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35),[35,40),[40,45)的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为 ( )
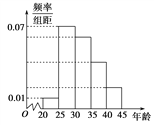
A. 0.04 B. 0.06
C. 0.2 D. 0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的编号之和等于7则中一等奖,等于6或5则中二等奖,等于4则中三等奖,其余结果为不中奖.
(1)求中二等奖的概率.
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘走私船,在
处有一艘走私船,在![]() 处北偏西
处北偏西![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘缉私艇奉命以
处有一艘缉私艇奉命以![]() 海里/时的速度追截走私船,此时,走私船正以
海里/时的速度追截走私船,此时,走私船正以![]() 海里/时的速度从
海里/时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.
方向逃窜.
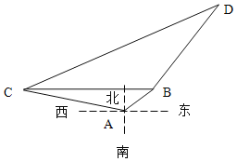
(1)问![]() 船与
船与![]() 船相距多少海里?
船相距多少海里?![]() 船在
船在![]() 船的什么方向?
船的什么方向?
(2)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数,
为参数, ![]() ),将曲线
),将曲线![]() 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线![]() .
.
(1)以原点为极点, ![]() 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() (
(![]() 为参数)与
为参数)与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产某种产品进行出售,当这种产品定价为每吨1000元时,每月可售出产品100吨.当每吨价格每增加20元时,月售出量将会减少1吨.产品每吨生产成本400元,月固定成本为20000元.
(Ⅰ)当产品每吨定价为1200元时,该公司月利润是多少?
(Ⅱ)当产品每吨定价为多少元时,该公司的月利润最大?最大月利润是多少?(利润=总收入-生产成本-固定成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com