分析:(1)平移向量的坐标等于平移后的坐标减平移前的坐标,因为题目中平移前、向量坐标均已给出,故直接代入即得答案.
(2)根据平移变换的口决“左加右减,上加下减”,平移向量
=(3,2),表示函数图象向右平移三个单位,再向上平移两个单位.
(3)根据平移变换的口决“左加右减,上加下减”,平移向量
=(3,2),表示函数图象向右平移三个单位,再向上平移两个单位.
解答:解:(1)平移前M(2,3),平移向量
=(3,2),
令N点的坐标为(x,y)
则x=2+3=5,y=3+2=5
故N点的坐标为(5,5)
(2)根据根据平移变换的口决“左加右减,上加下减”,
平移向量
=(3,2),表示函数图象向右平移三个单位,再向上平移两个单位.
则函数
y=2x+3的图象l按向量=(3,2)平移,求平移后的图象l′的函数解析式为y=2(x-3)+2=2x-4
(3)根据平移变换的口决“左加右减,上加下减”,
平移向量
=(3,2),表示函数图象向右平移三个单位,再向上平移两个单位.
则
y=x2的图象C按向量=(3,2)平移后的图象C′的解析式为y=(x-3)
2+2=x
2-6x+11
点评:平移向量中,平移前的点的坐标(a,b),与平移后的坐标(c,d)及平移向量坐标(h,k)之间的关系为:
平移向量
=(h,k)就是将函数的图象向右平移h个单位,再向上平移k个单位.再根据平移变换的口决“左加右减,上加下减”即可解答.



 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案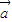 =(3,2)平移,求平移后对应点N的坐标.
=(3,2)平移,求平移后对应点N的坐标.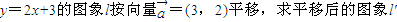 的函数解析式.
的函数解析式.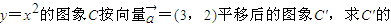 函数解析式.
函数解析式.