
| A. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | B. | (-$\frac{1}{8}$+k,$\frac{1}{8}$+k](k∈Z) | C. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | D. | [$\frac{1}{8}$+k,$\frac{3}{8}$+k)(k∈Z) |
分析 根据复合函数单调性之间的关系,进行求解即可.
解答 解:要求函数y=$lo{g}_{\frac{1}{2}}sin(2πx+\frac{π}{4})$的单调递减区间,即求出函数y=sin(2πx+$\frac{π}{4}$)的单调递增区间且sin(2πx+$\frac{π}{4}$)>0,
即2kπ<2πx+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,
即-$\frac{1}{8}$+k<x≤$\frac{1}{8}$+k,
即函数的单调递减区间为(-$\frac{1}{8}$+k,$\frac{1}{8}$+k].
故选:B
点评 本题主要考查函数单调区间的求解,利用复合函数单调性之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 18 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
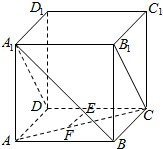 如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF.求证:EF∥平面A1B1CD.
如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF.求证:EF∥平面A1B1CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{{\sqrt{5}}}{2},2\sqrt{5}}]$ | B. | $({1,\sqrt{5}}]$ | C. | $[{\frac{{\sqrt{5}}}{2},\sqrt{5}}]$ | D. | $[{\sqrt{5},2\sqrt{5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
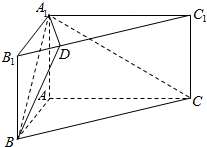 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com