
����Ŀ�����������������ҹ��Ŵ���ѧ�ɾ͵Ľܳ����������С�������л�������������⣬������Ի�����ҳ�ʸ��ʸ���Գˣ���֮������һ��������ǣ�����������㹫
ʽΪ�����������![]() ����������Բ�������Ϊ���ﻡ������Բ
����������Բ�������Ϊ���ﻡ������Բ
��������Ϊ������߶Σ����Ϊ�����ң�Χ�ɵ�ƽ��ͼ�Σ���ʽ�С��ҡ�ָ���ǻ�
���ҵij�����ʸ�����ڻ��ﻡ����Բ�İ뾶��Բ�ĵ������ҵľ���֮�����һ��
����ҳ�AB����6�ף��仡����ԲΪԲO��������������������㹫ʽ��ø�
��������Ϊ![]() ƽ���ף���cos��AOB�� �� ��
ƽ���ף���cos��AOB�� �� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �����Σ���
��������![]() .��
.��
![]() ����
����![]() ���е㣬ƽ��
���е㣬ƽ��![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.

��1����֤��![]() ��
��![]() ��
��
��2����![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() ����ƽ��
����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɵ������ǵ�����ֵ.
���ɵ������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������У� ![]() ��
�� ![]()
![]()
![]() ����
����![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ� ![]()
![]() ��
�� ![]() ��
��

��1��֤���� ![]() ��
��
��2��������![]() ��ƽ��ǵ�����ֵ��
��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������![]() ��,����
��,����![]() Ϊƽ���ı���,
Ϊƽ���ı���, ![]() Ϊ����
Ϊ����![]() ���е�.
���е�.
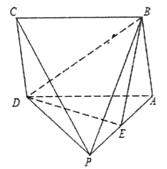
������֤: ![]() ��ƽ��
��ƽ��![]()
������![]() ,
,![]() ,
,
��֤:ƽ��![]()
![]() ƽ��
ƽ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() .
.
��1����![]() ʱ��
ʱ��![]() ��ֵ��
��ֵ��
��2��������![]() ��
��![]() ������ֻ��һ����㣬��
������ֻ��һ����㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��������Ϊ���˽���������ʳϰ�ߣ����ü���������ķ�����ȫУһ�꼶ѧ���н����˳������飬���������±���ʾ��
ϲ����Ʒ | ��ϲ����Ʒ | �ϼ� | |
�Ϸ�ѧ�� | 60 | 20 | 80 |
����ѧ�� | 10 | 10 | 20 |
�ϼ� | 70 | 30 | 100 |
��1�����ݱ������ݣ����Ƿ���95%�İ�����Ϊ���Ϸ�ѧ���ͱ���ѧ����ѡ����Ʒ����ʳϰ�߷����в��족��
��2�����ݣ�1���Ľ��ۣ����ܷ�������õĵ��鷽�����˽��У��ѧ��������ʳϰ�ߣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У���
�У���![]() Ϊ���㣬
Ϊ���㣬![]() ��ķǸ�����Ϊ���Ὠ���ļ�����ϵ�У�ֱ��
��ķǸ�����Ϊ���Ὠ���ļ�����ϵ�У�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��![]() ��������
��������![]() �IJ�������Ϊ
�IJ�������Ϊ
��1��д��ֱ��![]() ������
������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2������![]() ƽ����ֱ��
ƽ����ֱ��![]() ��ֱ��������
��ֱ��������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() �����
�����![]() �켣��ֱ�����귽�̣�
�켣��ֱ�����귽�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������![]() �У��ı���
�У��ı���![]() Ϊ���Σ���
������![]() ����������
Ϊ���������Σ�![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ����
����![]() ��
��![]() ,
,![]() ,
,![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣮
���е㣮

��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��3��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ���������Ϻ�����Ϊ
���������Ϻ�����Ϊ![]() �ĵ㵽�����߶���ľ�����õ㵽�������ߵľ�����ȡ�
�ĵ㵽�����߶���ľ�����õ㵽�������ߵľ�����ȡ�
��1����������![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��������
��������![]() ����
����![]() ���㣬��
���㣬��![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com