
【题目】已知函数![]() ,
,
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 且
且![]() ,设
,设![]() 是函数
是函数![]() 的零点.
的零点.
(i)证明:![]() 时存在唯一
时存在唯一![]() 且
且![]() ;
;
(ii)若![]() ,记
,记![]() ,证明:
,证明:![]() .
.
【答案】(1) 见解析;(2) (i)证明见解析.(2)(ii)证明见解析.
【解析】
(1)对![]() 求导,分析导函数的正负得单调区间;
求导,分析导函数的正负得单调区间;
(2) (i)根据(1)得函数的单调性,判断端点的函数的正负可得证;
(2) (ii)运用数列的裂项相消求和和不等式放缩技巧得证.
(1)由已知得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,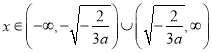 ,
,![]() ,
,
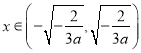 ,
,![]()
所以![]() 在
在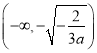 和
和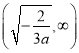 单调递减,
单调递减,
在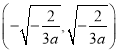 单调递增.
单调递增.
综上可得:
当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在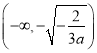 和
和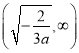 单调递减,
单调递减,
在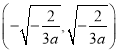 单调递增.
单调递增.
(2) (i)由(1)知:![]() ,
,![]() 在
在![]() 上单调递增;且
上单调递增;且![]() ,
,
所以![]() 在
在![]() 存在唯一的零点,
存在唯一的零点,
而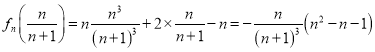 ,
,
且![]() 时,
时,![]() ,
,
所以:![]() 时存在唯一
时存在唯一![]() 且
且![]() ,
,
故得证.
(2) (ii)当![]() 时,
时,![]() ,所以
,所以 ![]()
所以![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
![]()
所以![]() ,所以
,所以![]() ,又
,又![]()
所以![]()
所以![]() ,
,
故得证.


科目:高中数学 来源: 题型:
【题目】下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
游戏1 | 游戏2 | 游戏3 |
袋中装有一个红球和一个白球 | 袋中装有2个红球和2个白球 | 袋中装有3个红球和1个白球 |
取1个球, | 取1个球,再取1个球 | 取1个球,再取1个球 |
取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
A.游戏1B.游戏2C.游戏3D.游戏2和游戏3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为公司在2017年8月9日推出的一款手机,已于9月19日正式上市.据统计发现该产品的广告费用x与销售额y的统计数据如下表:
广告费用x(百万元) | 4 | 2 | 3 | 5 |
销售额y(百万元) | 44 | 25 | 37 | 54 |
根据上表可得回归方程![]() 中的
中的![]() 为9.4,据此模型预测广告费用为6百万元时,销售额为( )
为9.4,据此模型预测广告费用为6百万元时,销售额为( )
A.61.5百万元B.62.5百万元C.63.5百万元D.65.0百万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种出口产品的关税税率![]() ,市场价格
,市场价格![]() (单位:千元)与市场供应量
(单位:千元)与市场供应量![]() (单位:万件)之间近似满足关系式:
(单位:万件)之间近似满足关系式:![]() ,其中
,其中![]() 、
、![]() 均为常数.当关税税率为
均为常数.当关税税率为![]() 时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为
时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为![]() 时,若市场价格为7千元,则市场供应量约为2万件.
时,若市场价格为7千元,则市场供应量约为2万件.
(1)试确定![]() 、
、![]() 的值;
的值;
(2)市场需求量![]() (单位:万件)与市场价格
(单位:万件)与市场价格![]() 近似满足关系式:
近似满足关系式:![]() .当
.当![]() 时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
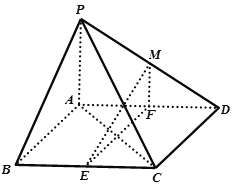
(1)若![]() 为
为![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一动点,现将
上一动点,现将![]() 沿
沿![]() 折起,使点
折起,使点![]() 在面
在面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,当点
上,当点![]() 从
从![]() 运动到
运动到![]() ,则点
,则点![]() 所形成轨迹的长度为( )
所形成轨迹的长度为( )
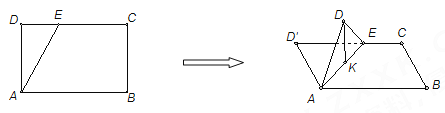
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高二学生视力情况进行调查,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
年级名次 是否近视 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)在(1)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: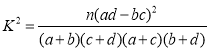
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com