
| A. | $-\frac{2b}{a}$ | B. | $-\frac{2a}{b}$ | C. | $-\frac{{\sqrt{2}b}}{a}$ | D. | $-\frac{{\sqrt{2}b}}{a}$ |
分析 设点M的坐标为(m,n),则点N的坐标为(-m,-n),且$\frac{{m}^{2}}{{a}^{2}}-\frac{{n}^{2}}{{b}^{2}}$=1,又设点P的坐标为(x,y),表示出直线PM和PN的斜率,求得两直线斜率乘积的表达式,把y和x的表达式代入发现结果与p无关,再利用基本不等式,即可得出结论.
解答 解:双曲线的类似的性质为:若M,N是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1上关于原点对称的两个点,点P是双曲线上的任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,kPM与kPN之积是与点P位置无关的定值.
下面给出证明:
设点M的坐标为(m,n),则点N的坐标为(-m,-n),且$\frac{{m}^{2}}{{a}^{2}}-\frac{{n}^{2}}{{b}^{2}}$=1.
又设点P的坐标为(x,y),由kPM=$\frac{y-n}{x-m}$,kPN=$\frac{y+n}{x+m}$得kPM•kPN=$\frac{{y}^{2}-{n}^{2}}{{x}^{2}-{m}^{2}}$,①
将y2=$\frac{{b}^{2}}{{a}^{2}}$x2-b2,n2=$\frac{{b}^{2}}{{a}^{2}}$m2-b2代入①式,得kPM•kPN=$\frac{{b}^{2}}{{a}^{2}}$(定值).
kPM<0、kPN<0,
∴kPM+kPN=-(-kPM-kPN)≤-$\frac{2b}{a}$,
∴kPM+kPN的最大值为-$\frac{2b}{a}$,
故选:A.
点评 本题主要考查了双曲线的性质,考查了学生综合分析问题和解决问题的能力,正确计算是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
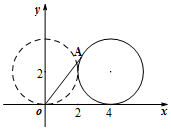 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com