
【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,已知
,已知![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,且
,且![]() ,求
,求![]() 边;
边;
(3)若![]() ,求
,求![]() 周长的最大值.
周长的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)由正弦定理化简题中给出的等式,再根据余弦定理可求出角![]() ;(2)由正弦定理和三角形的面积公司可求出
;(2)由正弦定理和三角形的面积公司可求出![]() ,再用余弦定理求出b边;(3)由余弦定理和基本不等式放缩即可求得三角形周长的最大值.
,再用余弦定理求出b边;(3)由余弦定理和基本不等式放缩即可求得三角形周长的最大值.
试题解析:
(1) ![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]()
所以![]() ,
,
所以![]() .
.
(2)由正弦定理得: ![]() ,
,
又![]() ,得
,得![]() ,所以
,所以![]() ,所以
,所以![]()
又由余弦定理: ![]()
所以![]()
(3)由余弦定理:
![]()
所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
故![]() ,即周长最大值为
,即周长最大值为![]() .
.
点睛:本题考查正余弦定理解决三角形问题以及基本不等式的应用. 在用基本不等式求最值时,应具备三个条件:一正二定三相等.①一正:关系式中,各项均为正数;②二定:关系式中,含变量的各项的和或积必须有一个为定值;③三相等:含变量的各项均相等,取得最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足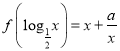 为常数
为常数
(1)求函数f(x)的表达式;
(2)如果f(x)为偶函数,求a的值;
(3)当f(x)为偶函数时,若方程f(x)=m有两个实数根x1,x2;其中x1<0,0<x2<1;求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题 ①设回归方程为 ![]() =3﹣3x,则变量x增加一个单位时,y平均增加3个单位;
=3﹣3x,则变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N (1,σ2) (σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对一切实数x,y均有f(x+y)﹣f(y)=(x+2y+2)x成立,且f(2)=12.
(1)求f(0)的值;
(2)在(1,4)上存在x0∈R,使得f(x0)﹣8=ax0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,AB=2,AD= ![]() ,∠DAB=
,∠DAB= ![]() ,PD⊥AD,PD⊥DC.
,PD⊥AD,PD⊥DC.
(Ⅰ)证明:BC⊥平面PBD;
(Ⅱ)若二面角P﹣BC﹣D为 ![]() ,求AP与平面PBC所成角的正弦值.
,求AP与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代中国数学辉煌灿烂,在《张丘建算经》中记载:“今有十等人,大官甲等十人官赐金,以等次差降之.上三人先入,得金四斤持出;下四人后入,得金三斤持出;中央三人未到者,亦依等次更给.问:各得金几何及未到三人复应得金几何?”则该问题中未到三人共得金多少斤?( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|).
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有车牌尾号为![]() 的汽车
的汽车![]() 和尾号为
和尾号为![]() 的汽车
的汽车![]() ,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日,
,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日, ![]() 车日出车频率
车日出车频率![]() ,
, ![]() 车日出车频率
车日出车频率![]() .该地区汽车限行规定如下:
.该地区汽车限行规定如下:
车尾号 |
|
|
|
|
|
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且![]() ,
, ![]() 两车出车相互独立.
两车出车相互独立.
(I)求该单位在星期一恰好出车一台的概率.
(II)设![]() 表示该单位在星期一与星期二两天的出车台数之和,求
表示该单位在星期一与星期二两天的出车台数之和,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com