
【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】某校高三共有800名学生,为了解学生3月月考生物测试情况,根据男女学生人数差异较大,从中随机抽取了200名学生,记录他们的分数,并整理得如图频率分布直方图.
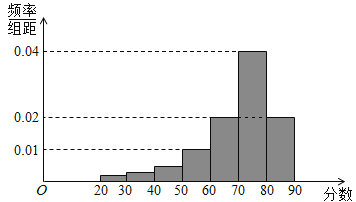
(1)若成绩不低于60分的为及格,成绩不低于80分的为优秀,试估计总体中合格的有多少人?优秀的有多少人?
(2)已知样本中有一半的女生分数不小于80,且样本中不低于80分的男女生人数之比2:3,试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2≥1}, ![]() ,则A∩(RB)=( )
,则A∩(RB)=( )
A.(2,+∞)
B.(﹣∞,﹣1]∪(2,+∞)
C.(﹣∞,﹣1)∪(2,+∞)
D.[﹣1,0]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
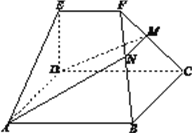
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对边分别为a,b,c且acosC,bcosB,ccosA成等差数列.
(1)求B的值;
(2)求2sin2A﹣1+cos(A﹣C)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
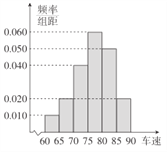
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为![]() (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
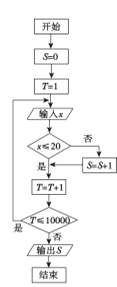
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n , 求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com