
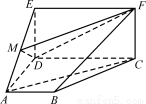
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90?,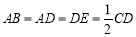 ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
(1)详见解析;(2)1:4.
【解析】
试题分析:(1)要使得AC∥平面DMF,需要使得AC平行平面DMF内的一条直线.为了找这条直线,需要作一个过AC而与平面DMF相交的平面.为此,连结CE,交DF于N,连结MN,这样只要AC∥MN即可.因为N为线段DF的中点,所以只需M是线段AE的中点即可.

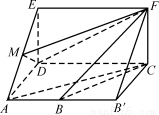
(2)一般地,求不规则的几何体的体积,可将其割为规则的几何体或补为规则的几何体.在本题中,可将几何体ADE-BCF补成三棱柱ADE-B?CF,如图.这样利用柱体和锥体的体积公式即可得其体积之比.
(1)当M是线段AE的中点时,AC∥平面DMF.
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN 平面DMF,又AC
平面DMF,又AC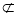 平面DMF,
平面DMF,
所以AC∥平面DMF. 4分
(2)如图,将几何体ADE-BCF补成三棱柱ADE-B?CF,

三棱柱ADE-B?CF的体积为 ,
,
则几何体ADE-BCF的体积
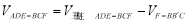 =
=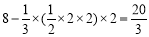 .
.
三棱锥F-DEM的体积V三棱锥M-DEF=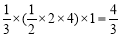 ,
,
故两部分的体积之比为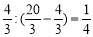 (答14,4,41均可). 12分
(答14,4,41均可). 12分
考点:1、空间线面关系;2、几何体的体积.


科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考文科数学试卷(解析版) 题型:选择题
已知ω>0,0<φ<π,直线x=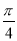 和x=
和x=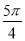 是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( )
是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( )
(A)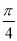 (B)
(B)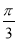 (C)
(C)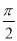 (D)
(D)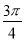
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:选择题
已知函数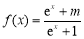 ,若
,若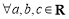 ,
,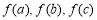 为某一个三角形的边长,则实数m的取值范围是( )
为某一个三角形的边长,则实数m的取值范围是( )
(A)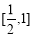 (B)
(B)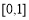 (C)
(C)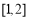 (D)
(D)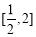
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:选择题
下列说法正确的是( )
(A)“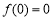 ”是“函数
”是“函数 是奇函数”的充要条件
是奇函数”的充要条件
(B)若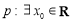 ,
,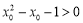 ,则
,则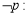
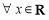 ,
,
(C)若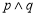 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
(D)“若 ,则
,则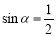 ”的否命题是“若
”的否命题是“若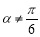 ,则
,则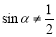 ”
”
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:填空题
图中的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:选择题
已知函数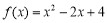 在区间
在区间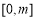 (
(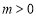 )上的最大值为4,最小值为3,则实数m的取值范围是( )
)上的最大值为4,最小值为3,则实数m的取值范围是( )
(A)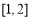 (B)
(B)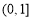 (C)
(C)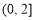 (D)
(D)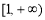
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三二诊模拟文科数学试卷(解析版) 题型:填空题
一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com