
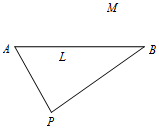
 �ұ߷��ֽӵ��鱨���ں���AB����ֱ��l��һ���M������˽�Ż��ڽ��н�����߷���Ѹ���ɳ���ͧǰȥ�Ѳ�����ͼ����֪��ͧ����λ����l����һ����ͷP����PA=8���PB=10�����APB=60�㣮
�ұ߷��ֽӵ��鱨���ں���AB����ֱ��l��һ���M������˽�Ż��ڽ��н�����߷���Ѹ���ɳ���ͧǰȥ�Ѳ�����ͼ����֪��ͧ����λ����l����һ����ͷP����PA=8���PB=10�����APB=60�㣮���� ��1����������ϵ������˫���ߵĶ��壬�ɵý��ۣ�
��2����˽����ֱ��l����࣬���ڣ�1�������ߵ���������ʱ��·��P��A��M��̣�
��� �⣺��1��������ͼ��ʾ������ϵ��|MA|-|MB|=2��
��M�Ĺ켣��˫���ߵ���֧��|AB|=$\sqrt{64+100-80}$=2$\sqrt{21}$��
��$a=1��c=\sqrt{21}��{b}^{2}=20$��
��M�Ĺ켣������${x}^{2}-\frac{{y}^{2}}{20}$=1��x��1��y��0����
��2����˽����ֱ��l����࣬���ڣ�1�������ߵ���������ʱ��·��P��A��M��̣�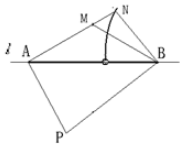
���ɣ���AM���ӳ����루1�������߽��ڵ�N����PA+AN=PB+BN��
PA+AM=PA+AN-MN=PB+BN-MN��PB+BM��
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬����˫���ߵĶ����뷽�̣������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��3 | B�� | 3��-1 | C�� | -1��3 | D�� | 0��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2] | B�� | [-2��-1] | C�� | [-1��0�� | D�� | ��-�ޣ�0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 24 | C�� | 120 | D�� | 720 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3��a2��a��0����a��1�� | B�� | 0.30.8��0.30.7 | C�� | ��-1��e-1 | D�� | log34��log43 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}f'��1��$ | B�� | 3f'��1�� | C�� | f'��1�� | D�� | f'��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com