
【题目】已知Sn为数列{an}的前n项和,且an>0,an2+an=2Sn .
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,记Tn=b12b32…b2n﹣12 , 求证:Tn≥
,记Tn=b12b32…b2n﹣12 , 求证:Tn≥ ![]() .
.
【答案】
(1)解:∵an2+an=2Sn,
∴an﹣12+an﹣1=2Sn﹣1,
∴an2+an﹣an﹣12﹣an﹣1=2an,
∴(an+an﹣1)(an﹣an﹣1﹣1)=0,
∵an>0,
∴an﹣an﹣1﹣1=0,
∴an﹣an﹣1=1,
∵n=1时
∴a12+a1=2S1=2a1,
解得a1=1,
∴数列{an}是以为首项以1为公差的等差数列,
∴an=1+(n﹣1)=n
(2)解:∵bn= ![]() =
= ![]() ,
,
∴数列{bn}是递增数列,
∴b2n>b2n﹣1,
∴b2nb2n﹣1>(b2n﹣1)2,
∴Tn=b12b32…b2n﹣12≥b1b1b2b3b4…b2n= ![]() ×
× ![]() ×
× ![]() ×
× ![]() ×…×
×…× ![]() ×
× ![]() =
= ![]() ,当n=1时取等号,
,当n=1时取等号,
∴Tn≥ ![]()
【解析】(1)利用递推关系可得an2+an=2Sn , an﹣12+an﹣1=2Sn﹣1 , 两式相减化简后得到an﹣an﹣1=1,继而得到数列{an}是以为首项以1为公差的等差数列,求出通项公式即可(2)bn= ![]() =
= ![]() ,数列{bn}是递增数列,利用放缩法即可证明.
,数列{bn}是递增数列,利用放缩法即可证明.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系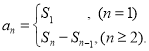 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


科目:高中数学 来源: 题型:
【题目】一个路口的红绿灯,红灯亮的时间为40秒,黄灯亮的时间为5秒,绿灯亮的时间为50秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?
(1)红灯;
(2)黄灯;
(3)不是红灯.
查看答案和解析>>
科目:高中数学 来源: 题型:
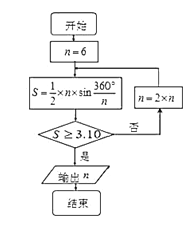
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
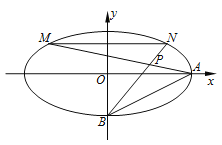
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的右、下顶点,且
的右、下顶点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
, ![]() .
.
(i) 若![]() ,
, ![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
(ii) 求证: ![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了![]() 位市民对共享单车的情况逬行问卷调査,并根根据其满意度评分值(滿分
位市民对共享单车的情况逬行问卷调査,并根根据其满意度评分值(滿分![]() 分)制作的茎叶图如图所示:
分)制作的茎叶图如图所示:
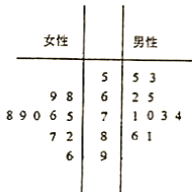
(1)分别计算男性打分的平均数和女性打分的中位数;
(2)从打分在![]() 分以下(不含
分以下(不含![]() 分)的市民抽取
分)的市民抽取![]() 人,求有女性被抽中的概率.
人,求有女性被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值;
的值;
(2)若![]() 成等差数列,
成等差数列,
①求数列![]() 的通项公式;
的通项公式;
②在![]() 与
与![]() 间插入
间插入![]() 个正数,共同组成公比为
个正数,共同组成公比为![]() 的等比数列,若不等式
的等比数列,若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com