
【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
【答案】(1)1440(2)3600(3)1440(4)4320
【解析】试题分析:本题主要考查排列问题中的特殊解题方法,解决“相邻”问题用“捆绑法”,利用整体思想,解题的思路是先整体、再局部;解决“不相邻”问题用“插空法”,也就是先排可以相邻的元素,再将要求不相邻的元素插入空中;用“间接法”解题,先不用考虑限制条件,计算出排列的总数,再减去不符合要求的排列数.
试题解析:(1)(捆绑法)将甲、乙两人“捆绑”为一个元素,与其余5人全排列,共有![]() 种排法,甲、乙两人可交换位置,有
种排法,甲、乙两人可交换位置,有![]() 种排法,故共有
种排法,故共有![]() (种)排法.
(种)排法.
(2)方法一(间接法)7人任意排列,有![]() 种排法,甲、乙两人相邻的排法有
种排法,甲、乙两人相邻的排法有![]() 种,故甲、乙不相邻的排法有
种,故甲、乙不相邻的排法有![]() (种).
(种).
方法二(插空法)将其余5人全排列,有![]() 种排法,5人之间及两端共有6个位置,任选2个排甲、乙两人,有
种排法,5人之间及两端共有6个位置,任选2个排甲、乙两人,有![]() 种排法,故共有
种排法,故共有![]() (种)排法.
(种)排法.
(3)(插空法)将其余4人拍好,有![]() 种排法,将甲、乙、丙插入5个空中,有
种排法,将甲、乙、丙插入5个空中,有![]() 种排法.故共有
种排法.故共有![]() (种)排法.
(种)排法.
(4)(间接法)![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】(1)求![]() 的展开式中
的展开式中![]() 的系数及展开式中各项系数之和;
的系数及展开式中各项系数之和;
(2)从0,2,3,4,5,6这6个数字中任取4个组成一个无重复数字的四位数,求满足条件的四位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表和频率分布直方图,回答下面问题:
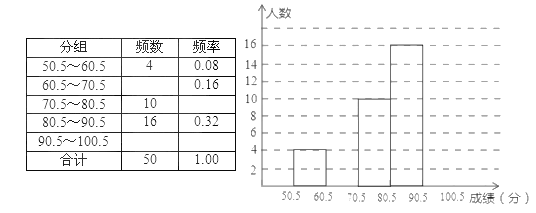
(1)结合图表信息,补全频率分布直方图;
(2)对于参加这次竞赛的900名学生,估计成绩不低于76分的约有多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: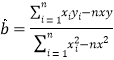 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
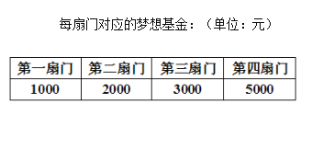
【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对![]() 号
号![]() 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:![]() ;
;![]() (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.
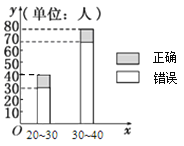
(1)写出![]() 列联表:判断是否有
列联表:判断是否有![]() 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?
说明你的理由.(下面的临界值表供参考)

(2)若某选手能正确回答第一、二、三、四扇门的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是![]() ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(参考公式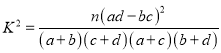 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的两个焦点为
)的两个焦点为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
, ![]() 在椭圆上,
在椭圆上, ![]() 在线段
在线段![]() 上,且
上,且![]() 的周长等于
的周长等于![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过圆![]() :
: ![]() 上任意一点
上任意一点![]() 作椭圆
作椭圆![]() 的两条切线
的两条切线![]() 和
和![]() 与圆
与圆![]() 交于点
交于点![]() ,
, ![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com