
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C, AB=3,BC=5.
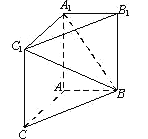
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)求点C到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)第(1)问,直接转化成平面ABC⊥平面AA1C1C. (2)利用空间向量法求二面角A1-BC1-B1的余弦值. (3)利用空间向量法求点C到平面![]() 的距离.
的距离.
试题解析:
证明:(1)因为![]() 为正方形,所以
为正方形,所以![]() .
.
因为平面ABC⊥平面AA1C1C,且平面ABC![]() 平面AA1C1C
平面AA1C1C ![]() ,所以
,所以![]() ⊥平面ABC.
⊥平面ABC.
(2)由(1)知, ![]() ⊥AC,
⊥AC, ![]() ⊥AB.
⊥AB.
由题意知![]() ,所以
,所以![]() .
.
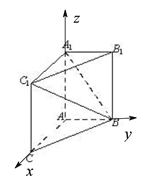
如图,以A为原点建立空间直角坐标系![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则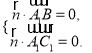 即
即![]()
令![]() ,则
,则![]() ,所以
,所以![]() .
.
同理可得,平面![]() 的法向量为
的法向量为![]() .
.
所以![]() .
.
由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为![]() .
.
(3)由(2)知平面![]() 的法向量为
的法向量为![]() ,
, ![]()
所以点C到平面![]() 距离
距离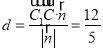 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
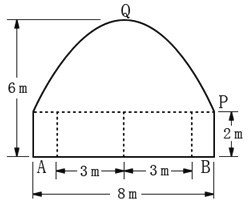
【题目】如图,一隧道内设双行线路,其截面由一长方形和一抛物线构成。为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部(抛物线)在竖直方向上的高度之差至少为0.5m,若行车道总宽度AB为6m,请计算通过隧道的车辆的限制高度(精确度为0.1m)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为
与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为![]()

(1)求椭圆![]() 的离心率;
的离心率;
(2) 设点C、D、F2分别为椭圆![]() 的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆
的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆![]() 相交于M、N 两点,若
相交于M、N 两点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).

(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把单位正方体的六个面分别染上6种颜色,并画上个数不同的金鸡,各面的颜色与鸡的个数对应如表:
面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过点M的直线与抛物线交于A,B两点,设A(x1 , y1)到准线l的距离d=2λp(λ>0) 
(1)若y1=d=3,求抛物线的标准方程;
(2)若 ![]() +λ
+λ ![]() =
= ![]() ,求证:直线AB的斜率的平方为定值.
,求证:直线AB的斜率的平方为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com