[题目]如图.正三棱锥A﹣BCD的侧棱长为2.底面BCD的边长为2 .E.分别为BC.BD的中点.则三棱锥A﹣BEF的外接球的半径R= . 内切球半径r= ．题目和参考答案——青夏教育精英家教网—

【题目】如图，正三棱锥A﹣BCD的侧棱长为2，底面BCD的边长为2 ，E，分别为BC，BD的中点，则三棱锥A﹣BEF的外接球的半径R= ，内切球半径r= ．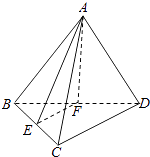

【答案】1；2﹣
【解析】解：设三棱锥A﹣BEF的外接球的球心为O，则O在平面BEF上的射影O′为△BEF的中心，
∴BO′= × =
∵A到平面BCD的距离为 = ，
∴三棱锥A﹣BEF的外接球的半径R= =1，
三棱锥A﹣BEF的体积V= = ，
又S= +2× + =2+ ，
∴ = （2+ ）r，
∴r=2﹣ ．
所以答案是：1，2﹣ ．
【考点精析】解答此题的关键在于理解球内接多面体的相关知识，掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某同学在利用“五点法”作函数f（x）=Asin（ωx+）+t（其中A＞0，）的图象时，列出了如表格中的部分数据．

x
ωx+	0		π		2π
f（x）	2	6	2	﹣2	2

（1）请将表格补充完整，并写出f（x）的解析式．
（2）若，求f（x）的最大值与最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=x+x2 ．
（1）求x＜0时，f（x）的解析式；
（2）问是否存在这样的非负数a，b，当x∈[a，b]时，f（x）的值域为[4a﹣2，6b﹣6]？若存在，求出所有的a，b值；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边．
（1）若△ABC面积S△ABC= ，c=2，A=60°，求a、b的值；
（2）若a=ccosB，且b=csinA，试判断△ABC的形状．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于函数f（x），若在定义域内存在实数x，满足f（﹣x）=﹣f（x），则称f（x）为“局部奇函数”．（I）已知二次函数f（x）=ax2+2bx﹣3a（a，b∈R），试判断f（x）是否为“局部奇函数”？并说明理由；
（II）设f（x）=2x+m﹣1是定义在[﹣1，2]上的“局部奇函数”，求实数m的取值范围；
（III）设f（x）=4x﹣m2x+1+m2﹣3，若f（x）不是定义域R上的“局部奇函数”，求实数m的取值范围．