
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】社会公众人物的言行一定程度上影响着年轻人的人生观、价值观.某媒体机构为了解大学生对影视、歌星以及著名主持人方面的新闻(简称:“星闻”)的关注情况,随机调查了某大学的![]() 位大学生,得到信息如下表:
位大学生,得到信息如下表:
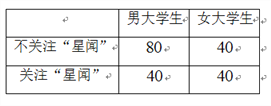
(Ⅰ)从所抽取的![]() 人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;
人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;
(Ⅱ)是否有![]() 以上的把握认为“关注‘星闻’与性别有关”,并说明理由;
以上的把握认为“关注‘星闻’与性别有关”,并说明理由;
(Ⅲ)把以上的频率视为概率,若从该大学随机抽取![]() 位男大学生,设这
位男大学生,设这![]() 人中关注“星闻”的人数为
人中关注“星闻”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 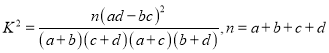 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
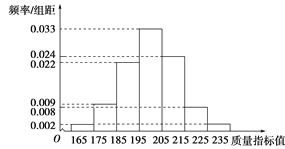
(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表);
和样本方差s2(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
(ⅰ)利用该正态分布,求P(187.8<Z<212.2);
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数.利用(ⅰ)的结果,求E(X).
附: ![]() ≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届云南省云南师范大学附属中学高三高考适应性月考(五)文数】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线斜率为1,求函数
处的切线斜率为1,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数
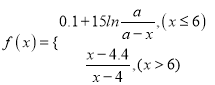
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.

(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com