
【题目】已知数列{an}的前n项和为Sn , 且a1=a(a∈R),an+1= ![]() ,n∈N*;
,n∈N*;
(1)若0<an≤6,求证:0<an+1≤6;
(2)若a=5,求S2016;
(3)若a= ![]() (m∈N*),求S4m+2的值.
(m∈N*),求S4m+2的值.
【答案】
(1)解:当an∈(0,3]时,则an+1=2an∈(0,6],
当an∈(3,6]时,则an+1=an﹣3∈(0,3],
故an+1∈(0,6],
所以当0<an≤6时,总有0<an+1≤6
(2)解:a1=a=5时,a2=a1﹣3=2,a3=2a2=4,a4=a3﹣3=1,a5=2a4=2,a6=2a5=4,a7=a6﹣3=1,
∴数列{an}5,2,4,1,2,4,1,2,4,1,…,
∴从2项起,以3为周期的数列,其和为2+4+1=7,
∴S2016=5+7×671+2+4=4708
(3)解:由m∈N*,可得2m﹣1≥1,故a= ![]() ≤3,
≤3,
当1<k≤m时,2k﹣1a≤ ![]() =
= ![]() <
< ![]() =3.
=3.
故ak=2k﹣1a且am+1=2ma.又am+1= ![]() >3,
>3,
所以am+2=am+1﹣3=2ma﹣3=2m ![]() ﹣3=a.
﹣3=a.
故S4m+2=S4(m+1)﹣a4m+3﹣a4m+4=4(a1+a2+…+am+1)﹣(2m﹣1+2m)a
=4(1+2+…+2m)a﹣3×2m﹣1a=4(2m+1﹣1)a﹣3×2m﹣1a
=(2m+3﹣3﹣3×2m﹣1)a= ![]()
【解析】(1)分当an∈(0,3]时和当an∈(3,6]时,分别求出an+1的范围,得到要证的不等式.(2)根据递推公式得到,数列{an}5,2,4,1,2,4,1,2,4,1,…,从2项起,以3为周期的数列,即可求出答案.(3)通过解不等式判断出项的取值范围,从而判断出项之间的关系,选择合适的求和方法求出和.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F,C上一点
的焦点F,C上一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A,B两点,若直线AB中点的纵坐标为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1 , x2 , 求证:x1x2>e2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(1)证明:EM⊥BF;
(2)求平面 BEF 与平面ABC 所成的二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f (x)的定义域为D,如果存在非零常数T,对于任意 x∈D,都有f(x+T)=Tf (x),则称函数y=f(x)是“似周期函数”,非零常数T为函数y=f( x)的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”y=f(x)的“似周期”为﹣1,那么它是周期为2的周期函数;
②函数f(x)=x是“似周期函数”;
③函数f(x)=2x是“似周期函数”;
④如果函数f(x)=cosωx是“似周期函数”,那么“ω=kπ,k∈Z”.
其中是真命题的序号是 . (写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点列An(an , bn)(n∈N*)均为函数y=ax(a>0,a≠1)的图象上,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意连续三项能构成三角形的三边,则a的取值范围为( )
A.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
B.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
C.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin(x+
sin(x+ ![]() )cos(x﹣
)cos(x﹣ ![]() )﹣cos2x﹣
)﹣cos2x﹣ ![]() .
.
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在[﹣ ![]() ,
, ![]() π]上的最大值.
π]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为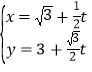 (t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2
(t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2![]() cosθ.
cosθ.
(1)求直线l的普通方程与曲线C的直角坐标方程。
(2)求出直线l与曲线C相交后的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com