
【题目】用![]() 表示一个小于或等于
表示一个小于或等于![]() 的最大整数.如:
的最大整数.如:![]() ,
,![]() ,
,![]() . 已知实数列
. 已知实数列![]() 、
、![]() 、
、![]() 对于所有非负整数
对于所有非负整数![]() 满足
满足![]() ,其中
,其中![]() 是任意一个非零实数.
是任意一个非零实数.
(Ⅰ)若![]() ,写出
,写出![]() 、
、![]() 、
、![]() ;
;
(Ⅱ)若![]() ,求数列
,求数列![]() 的最小值;
的最小值;
(Ⅲ)证明:存在非负整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
【答案】(Ⅰ)![]() ,
,![]() ,
,![]() ;(Ⅱ)最小值为
;(Ⅱ)最小值为![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】
(Ⅰ)由![]() ,代入可得
,代入可得![]() ,同理可得:
,同理可得:![]() 、
、![]() ;
;
(Ⅱ)由![]() ,可得
,可得![]() ,
,![]() ,设
,设![]() ,
,![]() ,可得
,可得![]() ,因此
,因此![]() ,
,![]() . 又因
. 又因![]() ,可得
,可得![]() ,
,![]() . 假设
. 假设![]() ,都有
,都有![]() 成立,可得:
成立,可得:![]() ,
,![]() ,利用累加求和方法可得
,利用累加求和方法可得![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() ,得出矛盾,
,得出矛盾,![]() ,从而可得出
,从而可得出![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,由(Ⅱ)知,存在
时,由(Ⅱ)知,存在![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,由此得出
,由此得出![]() ,
,![]() ,成立.;若
,成立.;若![]() ,
,![]() ,推导出数列
,推导出数列![]() 单调不减.由
单调不减.由![]() 是负整数,可知存在整数
是负整数,可知存在整数![]() 和负整数
和负整数![]() ,使得当
,使得当![]() 时,
时,![]() .所以,当
.所以,当![]() 时,
时,![]() ,转化为
,转化为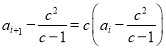 ,令
,令![]() ,即
,即![]() ,
,![]() .经过讨论:当
.经过讨论:当![]() 时,得证.当
时,得证.当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() ,则
,则![]() 有界,进而证明结论.
有界,进而证明结论.
(Ⅰ)![]() ,
,![]() ,
,
同理可得:![]() ,
,![]() ;
;
(Ⅱ)因![]() ,则
,则![]() ,所以
,所以![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() .
.
又因![]() ,则
,则![]() ,则
,则![]() ,
,![]() .
.
假设![]() ,都有
,都有![]() 成立,则
成立,则![]() ,
,
则![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
则![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() ,
,
这与假设矛盾,所以![]() ,
,![]() 不成立,
不成立,
即存在![]() ,
,![]() ,从而
,从而![]() 的最小值为
的最小值为![]() ;
;
(Ⅲ)当![]() 时,由(Ⅱ)知,存在
时,由(Ⅱ)知,存在![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,成立.
,成立.
当![]() 时,若存在
时,若存在![]() ,
,![]() ,则
,则![]() ,
,![]() ,得证;
,得证;
若![]() ,
,![]() ,则
,则![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,所以数列
,所以数列![]() 单调不减.
单调不减.
由于![]() 是负整数,所以存在整数m和负整数c,使得当
是负整数,所以存在整数m和负整数c,使得当![]() 时,
时,![]() .
.
所以,当![]() 时,
时,![]() ,则
,则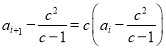 ,令
,令![]() ,
,
即![]() ,
,![]() .
.
当![]() 时,则
时,则![]() ,
,![]() ,则
,则![]() ,
,![]() ,得证.
,得证.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因当![]() 时,
时,![]() ,则
,则![]() ,则
,则![]() 有界,
有界,
所以![]() ,所以负整数
,所以负整数![]() .
.
![]() ,则
,则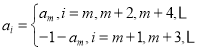
令![]() ,满足当
,满足当![]() 时,
时,![]() .
.
综上,存在非负整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
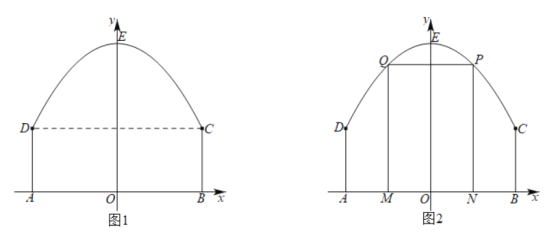
(1)求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
(2)如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”,将上述问题的所有正整数答案从小到大组成一个数列![]() ,则
,则![]() ______;
______;![]() ______.(注:三三数之余二是指此数被3除余2,例如“5”)
______.(注:三三数之余二是指此数被3除余2,例如“5”)
查看答案和解析>>
科目:高中数学 来源: 题型:
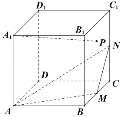
【题目】已知正方体![]() 的棱长为2,点
的棱长为2,点![]() 分别是棱
分别是棱![]() 的中点,则二面角
的中点,则二面角![]() 的余弦值为_________;若动点
的余弦值为_________;若动点![]() 在正方形
在正方形![]() (包括边界)内运动,且
(包括边界)内运动,且![]()
![]() 平面
平面![]() ,则线段
,则线段![]() 的长度范围是_________.
的长度范围是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数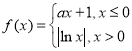 ,给出下列三个结论:
,给出下列三个结论:
①当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
②若函数![]() 无最小值,则
无最小值,则![]() 的取值范围为
的取值范围为![]() ;
;
③若![]() 且
且![]() ,则
,则![]() ,使得函数
,使得函数![]() .恰有3个零点
.恰有3个零点![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com