
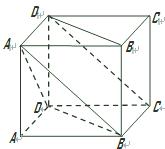
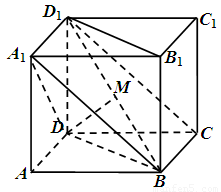
如图,在底面为平行四边形的四棱柱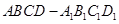 中,
中,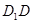
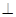 底面
底面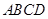 ,
,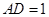 ,
,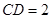 ,
,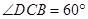 .
.
(Ⅰ)求证:平面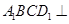 平面
平面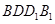 ;
;
(Ⅱ)若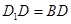 ,求四棱锥
,求四棱锥 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)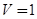 .
.
【解析】
试题分析:(Ⅰ)由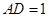 ,
,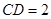 ,
,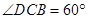 ,易得
,易得 ,从而
,从而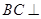 平面
平面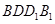 ,
,
由此可得平面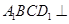 平面
平面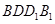 .
.
(Ⅱ)思路一、由(Ⅰ)知,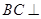 平面
平面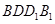 ,所以
,所以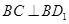 ,即
,即 是一个直角三角形,这样可得四边形
是一个直角三角形,这样可得四边形 的面积.
的面积.
又平面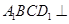 平面
平面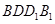 ,所以过D作
,所以过D作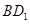 的垂线,该垂线即垂直于平面
的垂线,该垂线即垂直于平面 ,由此可得该棱锥的高,从而求得其体积.
,由此可得该棱锥的高,从而求得其体积.
思路二、将四棱锥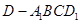 分割为以下两部分:三棱锥
分割为以下两部分:三棱锥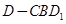 和
和 ,这两个三棱锥的体积相等,我们可先求其中的一个. 而三棱锥
,这两个三棱锥的体积相等,我们可先求其中的一个. 而三棱锥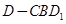 即为三棱锥
即为三棱锥 ,这个三棱锥的体积就很易求了.
,这个三棱锥的体积就很易求了.
试题解析:(Ⅰ)证明:在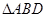 中,由余弦定理得:
中,由余弦定理得: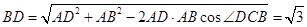 ,
,
所以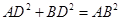 ,所以
,所以 ,即
,即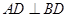 ,
3分
,
3分
又四边形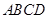 为平行四边形,所以
为平行四边形,所以 ,又
,又
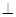 底面
底面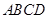 ,
,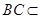 底面
底面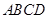 ,所以
,所以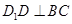 ,
,
又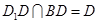 ,所以
,所以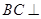 平面
平面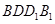 ,
5分
,
5分
又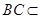 平面
平面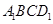 ,所以平面
,所以平面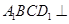 平面
平面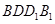 . 6分
. 6分
(Ⅱ)法一:连结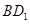 ,∵
,∵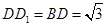 ,∴
,∴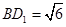
∵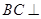 平面
平面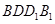 ,所以
,所以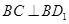 , 8分
, 8分
所以四边形 的面积
的面积 ,
10分
,
10分
取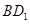 的中点
的中点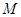 ,连结
,连结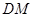 ,则
,则 ,且
,且 ,
,
又平面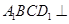 平面
平面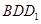 ,平面
,平面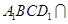 平面
平面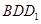
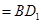 ,
,
所以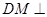 平面
平面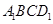 ,
,
所以四棱锥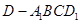 的体积:
的体积: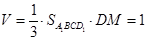 .
12分
.
12分
法二: 四棱锥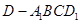 的体积
的体积 ,
8分
,
8分
而三棱锥 与三棱锥
与三棱锥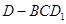 底面积和高均相等,
10分
底面积和高均相等,
10分
所以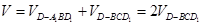
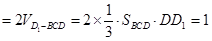 . 12分
. 12分
考点:1、空间两平面的垂直;2、空间几何体的体积.


科目:高中数学 来源: 题型:
 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=AC=2,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=AC=2,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com