
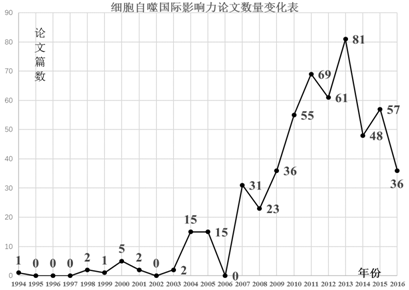
分析 (Ⅰ)设抽到2016年发表的论文为事件A,利用等可能事件概率计算公式能求出抽到2016年发表论文的概率.
(Ⅱ)设至少抽到一个“丰年”为事件B,利用列举法能求出至少一个“丰年”的概率.
(Ⅲ)81,48,57三个数方差最大,由此能求出结果.
解答 (共13分)
解:(Ⅰ)设抽到2016年发表的论文为事件A,依题意可知,
P(A)=$\frac{36}{540}$=$\frac{1}{15}$.…(5分)
(Ⅱ)设至少抽到一个“丰年”为事件B,依题意可知,
1994~2016的23年中随机抽取连续两年共有22种可能,
至少一个“丰年”的可能情况有:
2009~2010,2010~2011,2011~2012,2012~2013,2013~2014,2014~2015,2015~2016共计7种可能,
P(B)=$\frac{7}{22}$.…(11分)
(Ⅲ)81,48,57三个数方差最大,
所以从2013年开始,连续三年论文数方差最大.…(13分)
点评 本题考查概率与方差的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2)∪(3,+∞) | B. | (2,3) | C. | (-∞,2) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p为假 | B. | ¬p∧¬q为真 | C. | p∨q为真 | D. | q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 60 | C. | 30 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 42 | C. | 44 | D. | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com