
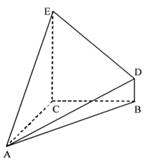
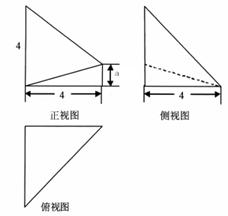
已知几何体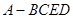 的三视图如图所示,其中俯视图和侧视图都是腰长为
的三视图如图所示,其中俯视图和侧视图都是腰长为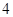 的等腰直角三角形,正视图为直角梯形.
的等腰直角三角形,正视图为直角梯形.
(1)若几何体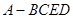 的体积为
的体积为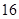 ,求实数
,求实数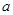 的值;
的值;
(2)若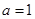 ,求异面直线
,求异面直线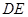 与
与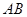 所成角的余弦值;
所成角的余弦值;
(3)是否存在实数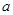 ,使得二面角
,使得二面角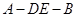 的平面角是
的平面角是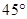 ,若存在,请求出
,若存在,请求出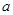 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
:(1)体积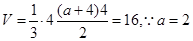 ;
;
(2)异面直线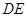 与
与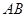 所成角的余弦值为
所成角的余弦值为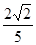 。……4分
。……4分
(3)不存在实数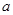 ,使得二面角
,使得二面角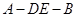 的平面角是
的平面角是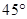 。
。
【解析】(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=1,则体积可以求得.
(2)求异面直线所成的角,一般有两种方法,一种是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.还有一种方法是向量法,即建立空间直角坐标系,利用向量的代数法和几何法求解.
(3)假设存在这样的点Q,使得AQ⊥BQ.
解法一:通过假设的推断、计算可知以O为圆心、以BC为直径的圆与DE相切.
解法二:在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,也可以建立空间直角坐标系,设定参量求解.这种解法的好处就是:1、解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.2、即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可
(1)体积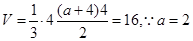 ; ……3分
; ……3分
(2) 法一:过点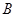 作
作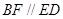 交
交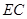 于
于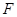 ,连接
,连接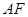 ,则
,则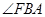 或其补角即为异面直线
或其补角即为异面直线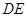 与
与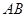 所成角,在
所成角,在 中,
中,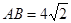 ,
,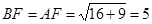 ,
,
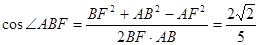 ;
;
即异面直线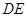 与
与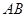 所成角的余弦值为
所成角的余弦值为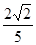 。……4分
。……4分
法二: 以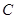 为原点,以
为原点,以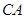 、
、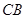 、
、 所在直线为
所在直线为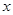 、
、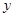 、
、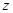 轴建立空间直角坐标系(图略),则
轴建立空间直角坐标系(图略),则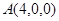 ,
,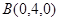 ,
,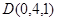 ,
,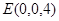 ,得
,得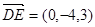 ,
,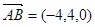 ,
,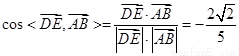 ,又异面直线
,又异面直线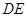 与
与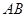 所成角为锐角,可得异面直线
所成角为锐角,可得异面直线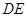 与
与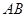 所成角的余弦值为
所成角的余弦值为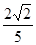 。
……4分
。
……4分
(3)平面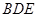 的法向量
的法向量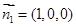 , ……1分
, ……1分
平面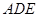 的法向量
的法向量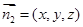 ,
,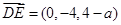 ,
,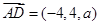 ,……1分
,……1分
由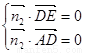 ,可得
,可得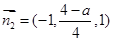 ,
,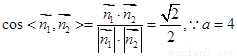 。…3分
。…3分
此时,与正视图为直角梯形条件不符,所以舍去,
因此不存在实数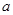 ,使得二面角
,使得二面角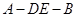 的平面角是
的平面角是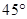


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com