Question

10．若函数f（x）=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点，则k的取值范围是（　　）

• A． （0，$\frac{1}{2}$]
• B． （$\frac{1}{4}$，$\frac{3}{4}$]
• C． [$\frac{1}{2}$，$\frac{3}{4}$）
• D． [$\frac{1}{4}$，1）

Answer 1

分析 若函数f（x）=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点，则函数y=$\sqrt{-{x}^{2}+4x-3}$与y=kx+k-1的图象有两个交点，数形结合可得答案．

解答 解：若函数f（x）=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点，
则函数y=$\sqrt{-{x}^{2}+4x-3}$与y=kx+k-1的图象有两个交点，
函数y=$\sqrt{-{x}^{2}+4x-3}$的图象是以（2，0）点为圆心，半径为1的半圆，
函数y=kx+k-1的图象表示恒过（-1，-1）点的直线，如下图所示：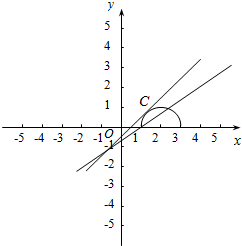

由图可得：函数y=kx+k-1图象过A（1，0）时，k=$\frac{1}{2}$，
函数y=kx+k-1图象与半圆切与C点时，$\frac{|2k+k-1|}{\sqrt{1+{k}^{2}}}=1$，解得：k=$\frac{3}{4}$，或k=0（舍去），
综上可得，k∈[$\frac{1}{2}$，$\frac{3}{4}$），
故选：C

点评 本题考查的知识点是函数的零点，直线与圆的位置关系，难度中档．