
分析 根据条件求出函数f(x)是周期函数,利用函数的周期性进行转化求解即可.
解答 解:∵f(x)=f(x-1)+f(x+1),
∴f(x+1)=f(x)+f(x+2),
即f(x)=f(x-1)+f(x)+f(x+2),
即f(x-1)+f(x+2)=0,
即f(x)+f(x+3)=0,
则f(x+3)=-f(x),
即f(x+6)=-f(x+3)=f(x),
当x>0时,函数f(x)是周期为6的周期函数,
则f(11)=f(6+5)=f(5)=1,
f(2015)=f(335×6+5)=f(5)=1,
则f(11)+f(2015)=1+1=2.
点评 本题主要考查函数值的计算,根据抽象函数的关系求出函数的周期性是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
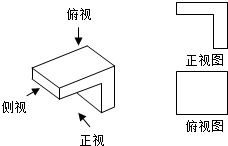 在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)
在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com