
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
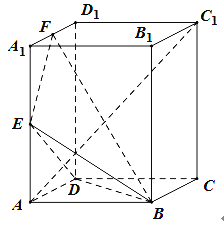
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)以点A为坐标原点,分别以AB,AD,AA1为x,y,z轴建立空间直角坐标系,利用向量法能证明AC1⊥平面BDE.
(2)求出平面BDE的法向量和平面FBE的法向量,二面角F﹣BE﹣D为锐二面角,利用向量法能求出二面角的余弦值.
(1)如图,以点A为坐标原点,分别以AB,AD,A![]() 为x,y,z轴建立空间直角坐标系
为x,y,z轴建立空间直角坐标系
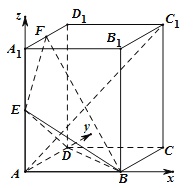
则A(0,0,0),B(1,0,0),D(0,1,0),E(0,0,![]() ),
),![]() (1,1,
(1,1,![]() ),
),
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() 与BE是平面BDE内两条相交直线
与BE是平面BDE内两条相交直线
![]() 平面BDE
平面BDE
(2)由(1)进一步可得F(0,![]() ),
),![]()
设平面BDE的法向量为![]() ,可取
,可取![]() ,
,
设平面FBE的法向量为![]() ,
,![]()
由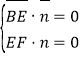 ,可得
,可得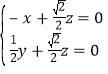 ,取x=1,可得
,取x=1,可得![]() (1,-2,
(1,-2,![]() )
)
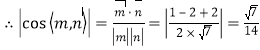 .
.
由于二面角F-BE-D为锐二面角,故所求的二面角的余弦值为![]()


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】对称轴为坐标轴的椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且直线
两点,且直线![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,则当
的斜率依次成等比数列,则当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中欧班列是推进与“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设.目前车站准备在某仓库外,利用其一侧原有墙体,建造一间墙高为3米,底面为12平方米,且背面靠墙的长方体形状的保管员室.由于此保管员室的后背靠墙,无需建造费用,因此甲工程队给出的报价为:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体报价为每平方米150元,屋顶和地面以及其他报价共计7200元.设屋子的左右两侧墙的长度均为![]() 米
米![]() .
.
(1)当左右两面墙的长度为多少时,甲工程队报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为![]() 元
元![]() ,若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求
,若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足以下两个条件:①不等式
满足以下两个条件:①不等式![]() 的解集是
的解集是![]() ②函数
②函数![]() 在
在![]() 上的最小值是3.
上的最小值是3.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若点![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() .
.
(ⅰ)求证:数列![]() 为等比数列
为等比数列
(ⅱ)令![]() ,是否存在正实数
,是否存在正实数![]() ,使不等式
,使不等式![]() 对于一切的
对于一切的![]() 恒成立?若存在,指出
恒成立?若存在,指出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两条生产线生产同种产品,现随机从这两条生产线上各抽取20件产品检测质量(单位:克),质量值落在![]() ,
, ![]() 的产品为三等品,质量值落在
的产品为三等品,质量值落在![]() ,
, ![]() 的产品为二等品,质量值落在
的产品为二等品,质量值落在![]() 的产品为一等品.下表为从两条生产线上各抽取的20件产品的质量检测情况,将频率视为概率,从甲生产线上随机抽取1件产品,为二等品的概率为0.2.
的产品为一等品.下表为从两条生产线上各抽取的20件产品的质量检测情况,将频率视为概率,从甲生产线上随机抽取1件产品,为二等品的概率为0.2.
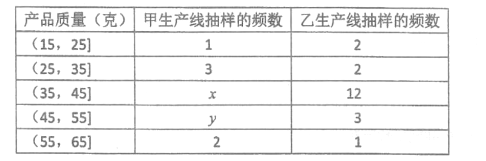
(1)求![]() 的值;
的值;
(2)现从两条生产线上的三等品中各抽取1件,求这两件产品的质量均在![]() 的概率;
的概率;
(3)估算甲生产线20个数据的中位数(保留3位有效数字).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com