
【题目】已知函数![]() 及关于
及关于![]() 的不等式
的不等式![]() .
.
(1)若该不等式的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)若该不等式的解集中有且只两个整数,求实数![]() 的取值范围.
的取值范围.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】某科技创新公司在第一年年初购买了一台价值昂贵的设备,该设备的第1年的维护费支出为20万元,从第2年到第6年,每年的维修费增加4万元,从第7年开始,每年维修费为上一年的125%.
(1)求第n年该设备的维修费![]() 的表达式;
的表达式;
(2)设![]() ,若
,若![]() 万元,则该设备继续使用,否则须在第n年对设备更新,求在第几年必须对该设备进行更新?
万元,则该设备继续使用,否则须在第n年对设备更新,求在第几年必须对该设备进行更新?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且a1=1,an+12=Sn+1+Sn .
(1)求{an}的通项公式;
(2)设bn=a2n﹣1![]() , 求数列{bn}的前n项和Tn .
, 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面坐标系内,O为坐标原点,向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点M为直线OP上的一个动点.
=(2,1),点M为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求向量
取最小值时,求向量 ![]() 的坐标;
的坐标;
(2)在点M满足(I)的条件下,求∠AMB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本p(x)=![]() 万元.
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量q(m)=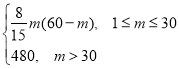 (单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
(单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com